
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Based on the graph of a function that I attached how do I Find the graph of its derivative
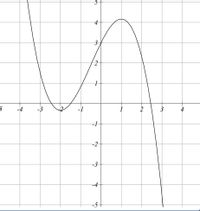
Transcribed Image Text:This image depicts the graph of a cubic polynomial function. The graph is plotted on a Cartesian plane with labeled axes.
### Description
- **Axes**:
- The horizontal axis is the x-axis, ranging from -5 to 5.
- The vertical axis is the y-axis, ranging from -5 to 5.
- **Curve**:
- The curve intersects the y-axis at approximately \( y = 0 \).
- Key points on the graph include a local minimum around \( x = -3 \) and a local maximum around \( x = 1 \).
- The function decreases from negative infinity, reaches a local minimum near \( (-3, -4) \), then increases to a local maximum around \( (1, 4) \), before decreasing again.
- **Behavior**:
- The function exhibits cubic behavior, changing direction twice to form a wave-like shape.
- It moves upwards as it approaches the local maximum, then downwards after passing it.
This graph can be used to illustrate concepts such as local maxima and minima, points of inflection, and the general shape and behavior of polynomial functions.
Expert Solution
arrow_forward
Step 1: Have a close look at the graph and write down the information you gather.
See from the given graph of the function , the graph becomes parallel to x axis at the points
Thus, the derivative becomes zero at and . That is,
Thus, has roots at .
Also see that, is an increasing function for . Thus,
Also see that, is a decreasing function for . Thus,
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Can i get help step by step with this problem?arrow_forwardPlease show all your work in a piece of paper. Thank youarrow_forwardWhat is another name for the derivative when looking at a function graphically? A triangle that must contain pairs of points whose slopes are the opposite, reciprocal of each other is what kind of triangle? And what would we say the lines are to each other?arrow_forward
- Having a hard time finding the derivative of this specific function. Need some help so I can double check and see what I am doing wrong. Thanks!arrow_forwardHow do you find the derivative of the product of two functionsthat are differentiable at a point?arrow_forwardfind the derivative of the question in the picture please show all workarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning