Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: 1. Draw the graph of the function defined by the equation z = sin 0 for values of 0 from -360° to…
A: z = sin theta is plotted below... The height of any point on Ferris wheel always follow the graph of…
Q: Graph the function y = - 4 sin Give the period and the amplitude. .... Choose the correct graph of…
A: We will find the period, amplitude and the graph as following.
Q: The graph below includes one complete cycle of the graph of an equation containing a trigonometric…
A:
Q: Determine the amplitude, period, and phase shift of the function.. Graph the function. y = 8 sin…
A: Given equation is, y=8sinπx-2 If the equation is of the form, y=Asin(Bx-C)+D Then the amplitude is,…
Q: Determine two equations for the graph below. One equation in terms of cosine and one in terms of…
A: We have given a graph and we have to find the equation in terms of sine and cosine. Form graph…
Q: The graph below includes one complete cycle of the graph of an equation containing a trigonometric…
A: Consider the given graph.We need to identify the equation containing trigonometry whose one complete…
Q: -1.0 4.0 -2.0
A: Given query is to find the function of the given graph.
Q: Find the equation to the following graph, and find the period and vertical shift.
A: Given,
Q: Determine a sine function and a cosine function for the graph below. 12
A: We have to determine a sine function and a cosine function for the given graph.
Question

The graph below is one complete cycle of the graph of an equation containing a trigonometric function. Find an equation to match the graph.

Hint: Think about the general form of the trig function and find the constants A: amplitude, B: period, C: phase(Horizontal) shift, D: Vertical Shift from the graph.

You can check your final answer by plotting the function that you build and comparing it with your given function. Provide as many details as possible.

 

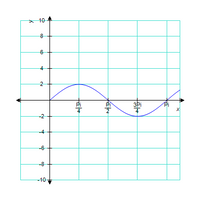
The image displays a graph of a trigonometric function, specifically a sine wave. The axes are labeled \(x\) and \(y\). ### Graph Details: - **XAxis (Horizontal)**: - The x-axis is marked with increments of \(\frac{\pi}{4}\) up to \(\pi\). - Key points are labeled as \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3\pi}{4}\), and \(\pi\). - **YAxis (Vertical)**: - The y-axis ranges from -10 to 10, with marks at every 2 units. ### Sine Wave Description: - The sine wave starts at the origin (0,0). - It reaches a maximum value slightly below \(\frac{\pi}{4}\). - It crosses the x-axis at \(\frac{\pi}{2}\). - It reaches a minimum value slightly below \(\frac{3\pi}{4}\). - The wave again crosses the x-axis at \(\pi\). This graph illustrates the periodic nature of sine functions, showing one complete cycle from 0 to \(\pi\).
expand button
Transcribed Image Text:The image displays a graph of a trigonometric function, specifically a sine wave. The axes are labeled \(x\) and \(y\). ### Graph Details: - **XAxis (Horizontal)**: - The x-axis is marked with increments of \(\frac{\pi}{4}\) up to \(\pi\). - Key points are labeled as \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3\pi}{4}\), and \(\pi\). - **YAxis (Vertical)**: - The y-axis ranges from -10 to 10, with marks at every 2 units. ### Sine Wave Description: - The sine wave starts at the origin (0,0). - It reaches a maximum value slightly below \(\frac{\pi}{4}\). - It crosses the x-axis at \(\frac{\pi}{2}\). - It reaches a minimum value slightly below \(\frac{3\pi}{4}\). - The wave again crosses the x-axis at \(\pi\). This graph illustrates the periodic nature of sine functions, showing one complete cycle from 0 to \(\pi\).
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
Step 3
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 3 steps

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS