
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Need the solution to number 3, please explain process to solution. Thank you

Transcribed Image Text:1. Apply a truth table to show each conclusion of following:
(a) ~(-p) = p
(b) ~(pVq) = (~p) ^ (~q)
2. Write down the converse, inverse and contra-positive of each of the following statements:
(a) For any real number x, if x >4, then x² > 16.
(b) If both a and b are integers, then their product ab is an integer.
3. Use logical equivalences to simplify each one of following
a) ((PA¬Q) V (PAQ)) ^Q (b)-((-p^q) v (p^-q)) v (p^q)
4. Negating the following statements:
(a) V primes p, p is odd.
(b) 3 a triangle T such that the sum of the angles equals 200°.
(c) For every square x there is a triangle y such that x and y have different colors.
(d) There exists a triangle y such that for every square x, x and y have different colors.
(e) V people p, if p is blond then p has blue eyes.
5. Construct a truth table to determine whether or not the argument is valid
(a)
(b)
pv (q vr)
יזר
pv q
p→qv (¬r)
q→ p^r
:p →r
6. Prove that
(a) 9n² + 3n-2 is even for any integer n.
(b) For all integers mann, m+nand m-nare either both odd or both even.
(c) There are real numbers such that √a + b = √a + √b.
(d) For all integers, if n is odd then n²is odd.
7. Show that the following statements are false:
(a) There is an integer n such that 2n² - 5n + 2 is a prime.
(b) If m and n are any two positive integers then mn > m + n.
Expert Solution
arrow_forward
Step 1: Recall some logical equivalence.
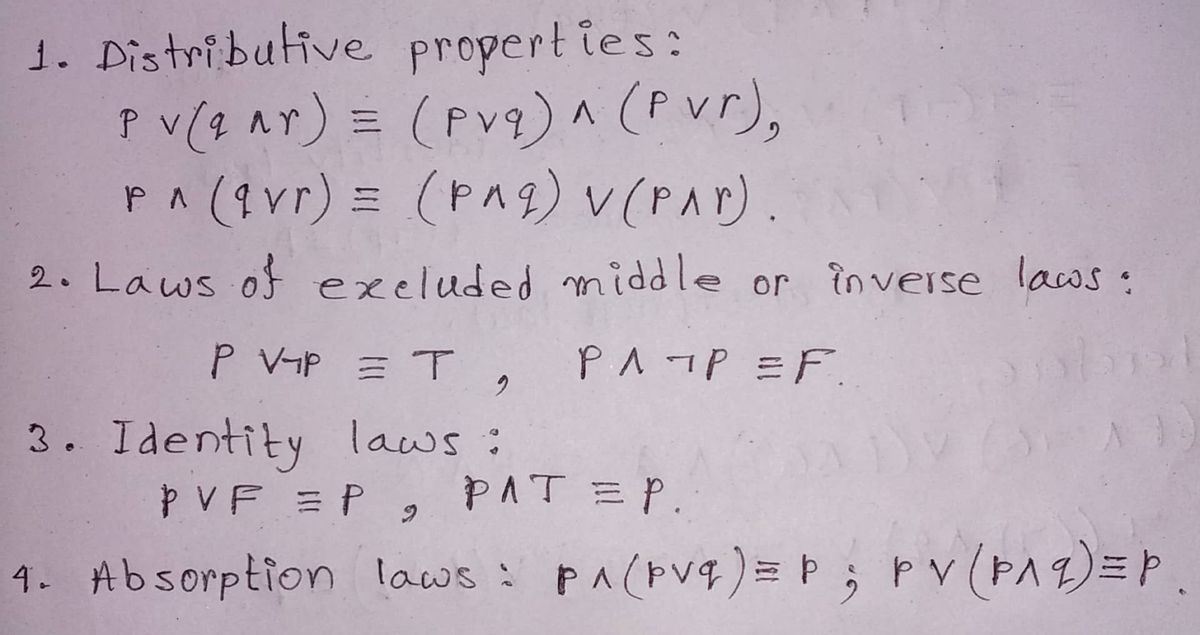
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Similar questions
- Use the table and info in both photos to solve for MSE, MSTR and F showing the answers in the appropriate box in the second photo. All info is in both photos. please answer clearly and explain. Thank youarrow_forwardA 3rd year student has 75 credits and a cumulative GPA of 2.88. This semester she is registered for 15 credits and hopes to raise his cumulative GPA to 3.00 and make the Dean’s List. Is it possible? What semester GPA will she need to accomplish that? Show your calculations or post a screenshot from your online GPA grade calculator.arrow_forwardHelp me pleasearrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

