
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Show that if P and Q are partitions of [a, b] such that Q is a refinement of P, then
S(f; P);;:, S(f; Q)
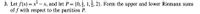
Transcribed Image Text:3. Let f(x)= x² – x, and let P :
of f with respect to the partition P.
{0,, 1, , 2}. Form the upper and lower Riemann sums
=
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Can I have this notation explained/rewrittenarrow_forwardFind the zeros of Q(x) = 5x - x² + 9 using the quadratic formula. Number of zeros: one X NOTE: Enter an exact value for the zero or round to three decimal places. be here to search X = -5+√11 2 O Xarrow_forwardConsider the relation R = {(1,1);(2,3);(3,5);(4,7)}. a. Prove that R is a function from {1,2,3,4} to {1,2,3,4;5,6,7}. b. Find a concise formula.arrow_forward
- Let A = {a, b, c, d} and let R = {(a, a), (a, b), (a, c), (a, d), (b, b), (b, c), (b, d), (c, c), (c, d), (d, d)} be arelation on A. Which of the properties reflexive, symmetric and transitive does the relation R possess? If Rdoes not possess one of these properties, explain why. How do I know where to stop? How do I know when I have proven transitivity? for example? I have difficulties with knowing if my prove is complete or notarrow_forward6. If A = {1, 2, 3} and B = {2, 3, 4}, and R is the relation xRy when x + y is divisible by 3, then R = O {1, 2), (2, 4)} all of these O {(1, 2), (2, 4), (3, 3)} O {1, 2), (3, 3)}arrow_forwardLet R, S, and T be sets. Let f: R -» S, and g: S -» T be maps. Assume we know that qf is 1-1 Must f be 1-1? Either prove that it is or find a counterexample (a) Must g be 1-1? Either prove that it is or find a counterexample (b)arrow_forward
- Let Pand Q be two predicates. Prove that 3x [ P(x) V Q(x) ] 3x P(x) V 3x Q(x)arrow_forwardDefine relations R 1 , … , R 6 on { 1 , 2 , 3 , 4 } by R 1 = { ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) } , R 2 = { ( 1 , 1 ) , ( 1 , 2 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) , ( 4 , 4 ) } , R 3 = { ( 2 , 4 ) , ( 4 , 2 ) } , R 4 = { ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) } , R 5 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 3 , 3 ) , ( 4 , 4 ) } , R 6 = { ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 1 ) , ( 3 , 4 ) } , Which of the following statements are correct? Check ALL correct answers below. A. R 2 is not transitive B. R 4 is antisymmetric C. R 5 is transitive D. R 6 is symmetric E. R 3 is transitive F. R 3 is reflexive G. R 3 is symmetric H. R 2 is reflexive I. R 4 is transitive J. R 5 is not reflexive K. R 4 is symmetric L. R 1 is not symmetric M. R 1 is reflexivearrow_forwardFind the transitive closure of the relation R={(1,2),(2,2), (2,3),(3,3)} on the set A={1,2,3}. Select one: O a. ={(2,2),(3,1),(2.2).(2,3).(3,3)}. O b. ={(1,1),(3,1),(2.2),(2,3),(3,3)}. O c. =((1,3),(3,1).(2,2), (2,3),(3,3)}. O d. ={(1,2),(1,3).(2,2),(2,3),(3,3)}. O e. ={(1,2),(3,1),(2,2),(2,3),(3,3)}.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

