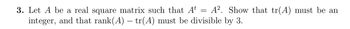
3. Let A be a real square matrix such that At = A². Show that tr(A) must be an integer, and that rank(A) - tr(A) must be divisible by 3.

Find the power of A for the matrixA19

A firm's total revenue function takes the form cQ2 + dQ. It is known that TR = 402 when Q = 3 and TR = 1098 when Q = 9. (a) Show that this information may be expressed as Ax = b where x = [c, d]¹, b = [402, 1098] and A is a 2x2 matrix which should be stated. (b) Use the matrix inverse method to work out the values of c and d, and hence write down the demand equation. (a) The coefficient matrix is (b) c= -2, d = 140 and the demand equation is P=Q+

1 Let A = 6 2 3 5 3 -1 1 4 Compute rank of A = nullity of A = rank of A + nullity of A = Check Answer

For matrices M and N, the 3rd column of NM is all zeros. Matrix M has 5 columns and none of them are all zero. Prove that the columns of N are linearly dependent.