3. For n e N, we define n! = (n)(n – 1)(n – 2)... (2)(1). E.g., 4! = (4)(3)(2)(1) = 24. Prove the following statements. (a) Let a, b, c E N. If a|b and alc, then a|(b + c). (b) Let n > 2 be a natural number. Use part (a) to prove that the numbers n! + 2, n! + 3,..., and n! +n are all composite. 1
3. For n e N, we define n! = (n)(n – 1)(n – 2)... (2)(1). E.g., 4! = (4)(3)(2)(1) = 24. Prove the following statements. (a) Let a, b, c E N. If a|b and alc, then a|(b + c). (b) Let n > 2 be a natural number. Use part (a) to prove that the numbers n! + 2, n! + 3,..., and n! +n are all composite. 1
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please help me i beg you
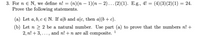
Transcribed Image Text:3. For n e N, we define n! = (n)(n – 1)(n – 2).. (2)(1). E.g., 4!
Prove the following statements.
(4)(3)(2)(1) = 24.
(a) Let a, b, c E N. If a|b and alc, then a|(b + c).
(b) Let n > 2 be a natural number. Use part (a) to prove that the numbers n! +
2, n! + 3, ..., and n! +n are all composite.
1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
