
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
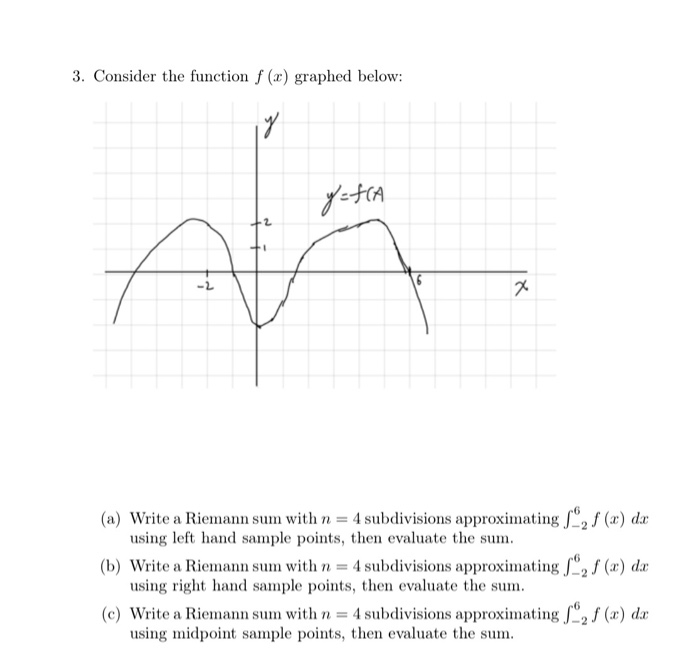
Transcribed Image Text:3. Consider the function f (x) graphed below:
yetiA
-2
(a) Write a Riemann sum with n = 4 subdivisions approximating ", f (æ) dx
using left hand sample points, then evaluate the sum.
(b) Write a Riemann sum with n = 4 subdivisions approximating "2 f (x) dæ
using right hand sample points, then evaluate the sum.
(c) Write a Riemann sum with n = 4 subdivisions approximating ", f (x) dx
using midpoint sample points, then evaluate the sum.
Expert Solution
arrow_forward
Step 1
Consider the provided graph,
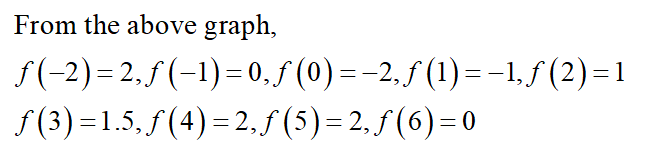
(a)
The Riemann sum with n = 4 using left hand sample points is given by,

arrow_forward
Step 2
(b)
The Riemann sum with n = 4 using right hand sample points is given by,

Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Similar questions
- (LT2.a) Express the following sum in Sigma notation: 3 4 5 6 + + + +...+ 33 34 36 38 (LT2.b) Consider the following graph of a function g: T -2 2 -2- 4 क 2 17 324 (b) Evaluate the definite integral f g(x) dx. -4 To demonstrate mastery you must show your work. 6 (a) Write out the left Riemann sum L5 for g on the interval [-4, 6] and compute its value.arrow_forwardGraph the function f(x) = x² − 1 over the interval [0, 2]. Partition the interval into four subintervals of equal length. Then add to your sketch the rectangles associated with the Riemann sum f(CK) Axk, given that c is the (a) left-hand endpoint, (b) right-hand endpoint, (c) midpoint of the kth subinterval. (a) Choose the correct graph below. O A. y (b) Choose the correct graph below. O A. 0 y (c) Choose the correct graph below. 4 B. 0 -2- 4 B. y 3 X X Q ... C. 4 -2- C. 4 0 D. 4 O D. k=1 tarrow_forward19er q gral (axa +Hy+2)dx a) Find the Riemann sum for this inmtegralarrow_forward
- No → C below +11 10 MMX MM Gar G SEG pl G SE + myopenmath.com/assess2/?cid=175669&aid=1.. The rectangles in the graph below illustrate a left endpoint Riemann sum for -x² f(x) = + 4x on the interval [3, 7] 2 9 8 7 6 5 4 3- 2 1 1 2 3 4 5 6 7 V The value of this left endpoint Riemann sum is 57.6 M-Ox OX ☐ ⠀ X 0 This Riemann sum is insufficient information of the area beneath the curve on [3, 7] Question Help: Video Message instructor O th.com/a Appro 117 Mc 0:27/5:14 n MEarrow_forwardConsider the function f(x) In this problem you will calculate Hint: Rn lim Rn n→∞ 2 2²2 -7. 4 4 • S" ( - ²² - 7) d 4 The summation inside the brackets is Rn which is the Riemann sum where the sample points are chosen to be the right-hand endpoints of each sub-interval. Calculate Rn for f(x) X² 7 dx by using the definition [*162) de - Hom [224] f(x) dx lim f(x₁) Ax i=1 - 7 on the interval [0, 4] and write your answer as a function of n without any summation signs. 4arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

