
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
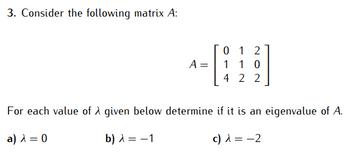
Transcribed Image Text:3. Consider the following matrix A:
A =
0 1 2
1 1 0
422
For each value of À given below determine if it is an eigenvalue of A.
a) λ = 0
b) λ = -1
c) λ = -2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Consider the following matrix: 1 -6 -6 -6 -4 -2 -2 8 -6 0 0 12 -1 -3 -3 0 A = a) Find the distinct eigenvalues of A, their multiplicities, and the corresponding number of basic eigenvectors. Number of Distinct Eigenvalues: 1 Eigenvalue: 0 has multiplicity 1 and corresponding number of basic eigenvectors 1 b) Determine whether the matrix A is diagonalizable. Conclusion: Official Time: A is diagonalizable A is not diagonalizable SUBMIT AND MARKarrow_forwardConsider the following matrices A and B and vector b. D)What is the algebraic and geometric multiplicities of the eigenvalues of A. f) Find A10b by writing b as linear combination of eigenvectors of A.G) Find a formula for Ak for all non-negative integers k.H) Use (g) to find A10b and compare it with what you found in (VI).I) Is A similar to B? If yes, find an invertible matrix such that P−1AP = B.arrow_forwardIf A is a 3 x 3 matrix which is diagonalizable and the following. three vectors are eigenvectors for 3 distinct eigenvalues of A, (0, 1, –1)", (2, 0, 3)7, (1, 1, -2)7, which of the following vectors could be the first column of a matrix P which diagonalizes A? A) (1, 1, -2)7 (B) (0, 0, 1)7 (C) (1, 0, 0)7 D) (0, 1, 0) (E) (-1,0, –1)7 (F) (1, 2, -3)7-(G) (0, 1, 1)7 H) (2, 0, -3)7arrow_forward
- Consider the following matrix: A = ..comm 3 0 0 00 03 0 -5 0-12 -3 12 000-2 a) Find the distinct eigenvalues of A, their multiplicities, and the corresponding number of basic eigenvectors. Number of Distinct Eigenvalues: 1 Eigenvalue: 0 has multiplicity 1 and corresponding number of basic eigenvectors 1 b) Determine whether the matrix A is diagonalizable. Conclusion: A is diagonalizable Question 13 A is diagonalizable A is not diagonalizable sk dom A in the diagonalizablo matrix boloy and P-1AP-D forarrow_forwardConsider the following matrix: A = 1 0-3 -9 -9 -2 2 -6 -18 -18 002 0 0 00 -3 -8 -9 003 10 11 a) Find the distinct eigenvalues of A, their multiplicities, and the dimensions of their associated eigenspaces. Number of Distinct Eigenvalues: 1 Eigenvalue: 0 has multiplicity 1 and eigenspace dimension 1 b) Determine whether the matrix A is diagonalizable. Conclusion: A is diagonalizable A is not diagonalizable SUBMIT AND MARK SAVE ANarrow_forwardFind bases for the eigenspaces associated with each eigenvalue of the matrix 3 0 0 -2 3-2 2 0 5 Find, if possible, a nonsingular matrix P such that P-¹AP is diagonal. A =arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

