Question
thumb_up100%
Part B - I don't understand why the last part of the line element has been excluded in the solution.

Transcribed Image Text:3. All three solutions in 2.b correspond to de Sitter spacetime (or a portion of it), with different
choices of coordinates. One way to define 4D de Sitter spacetime is via an embedding in 5D
Minkoswki spacetime,
4
ds² = −(dxº)² + dx³dx¹,
Σ
i=1
a) Consider the coordinates
xº
C2 _ R? sinh(T/),
where j = 2, 3, 4, the analogous exercise (Assignment 4) gives
−1
with constraint l² = − (xº)² + Σx²¹x².
x0 = {sinh(t/l), x² = y¹l cosh(t/l).
What is the constraint in terms of the coordinates y'? Determine the induced line element on de
Sitter spacetime. You should recover one of the cases in question 2.
b) With the coordinates
=
x¹
=
√12 R² cosh(T/l),
ds²
16² = -(1-1/²) α7² + (1-1/²)
dT²
4
1
i=1
dR² + R²d²(2).
x³ = R z³¹,
These are known as static coordinates. The cosmological horizon is located at R = l. How long
does it take for an observer at rest at R= 0 to receive a radially directed light ray emitted at
R = R₂ < l? Can a light ray be received from R =
=
=
Re > l?
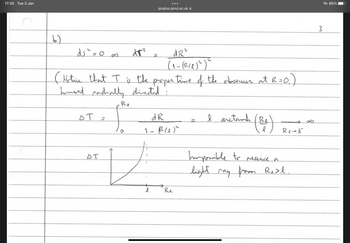
Transcribed Image Text:17:35 Tue 3 Jan
b)
ds ² = 0 =2
El
d12²
(₁- (RIR) ²)~
(Notice that I is the proper time of the observer at R=0.)
hinand radially directed"
I arctank (Re)
от
=
AT
Re
d#²
V
qmplus.qmul.ac.uk
dR
1-RUP
Re
Real
Impossible to receive a
light may from Real.
3
© 85%
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps

Knowledge Booster
Similar questions
- A 0.0545 kg chunk of an unknown metal that has been in boiling water for several minutes is quickly dropped into an insulating Styrofoam beaker that contains 0.462 kg of water at room temperature (20.0° C). After waiting for a few minutes, you observe that the water's temperature has reached a constant value of 22.0° C. Part A Assuming that the Styrofoam absorbs a negligibly small amount of heat and that no heat was lost to the surroundings, what is the specific heat of the metal? Express your answer in joules per kilogram-kelvin to three significant figures. ΑΣφ J/(kg · K) C = Submit Request Answer Part B Use the table below to identify the metal. Specific heat (c) Material J/(kg K) cal/(g K) Solids Lead 0.13 x 103 0.031 Mercury 0.14 × 103 0.033 Silver 0.23 × 103 0.056 Copper 0.39 × 10³ 0.093 Iron 0.47 x 103 0.112 Marble (CACO3) 0.88 × 10³ 0.21 Salt 0.88 × 103 0.21 Aluminum 0.91 × 103 0.217 Beryllium 1 97 x 103 0.471arrow_forwardConsider the following doping profile in the figure below: N₁- Na N. -x0 -N a x хо Figure 1: Problem 3 Doping Profile Sketch the charge density p(x), you may assume an abrupt junction Derive an expression for the electric fieldarrow_forwardQ2 part carrow_forward
- I need help with A and B for this problem. I want to see the detailed steps.arrow_forwardG.garrow_forwardHave you ever chewed on a wintergreen mint in front of a mirror in the dark? If you have, you may have noticed some sparks of light coming out of your mouth as you chewed on the candy; and, without knowing it, you have experienced a physical phenomenon called triboluminescence. In this problem you will analyze some of the key elements of triboluminescence in wintergreen candies. Part C Image that the radiation emitted by the nitrogen at a frequency of 8.88×1014 Hz is absorbed by an electron in a molecule of methyl salicylate. As a result, the electron in the wintergreen oil molecule jumps to an excited state. Before returning to its ground state, the electron drops an intermediate energy level, releasing two-thirds of the energy previously absorbed and emitting a photon. What is the wavelength Xw of the photon emitted by the wintergreen oil molecule? Express your answer in nanometers to three significant figures. ► View Available Hint(s) Aw= Submit [-] ΑΣΦ ? nmarrow_forward
arrow_back_ios
arrow_forward_ios