
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
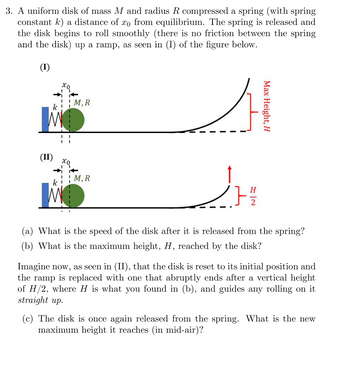
Transcribed Image Text:### Question 3: Dynamics of a Uniform Disk and Spring System
#### Problem Statement:
A uniform disk of mass \( M \) and radius \( R \) compresses a spring (with spring constant \( k \)) a distance of \( x_0 \) from equilibrium. Upon release, the disk begins to roll smoothly up a ramp, as depicted in diagram (I) below. There is no friction between the spring and the disk.
**Diagrams Explanation:**
**Diagram (I):**
- A spring is compressed by a uniform disk.
- The compressed distance is \( x_0 \).
- Upon release, the disk rolls up a ramp reaching a maximum height \( H \).
**Diagram (II):**
- The same initial setup, but the ramp now ends at a vertical height of \( H/2 \).
- Beyond this, the disk is guided vertically upward.
**Questions:**
**(a)** What is the speed of the disk after it is released from the spring?
**(b)** What is the maximum height \( H \) reached by the disk?
Imagine now, as seen in (II), that the disk is reset to its initial position and the ramp is replaced with one that abruptly ends after a vertical height of \( H/2 \), where \( H \) is what you found in (b), and guides any rolling on it straight up.
**(c)** The disk is once again released from the spring. What is the new maximum height it reaches (in mid-air)?
---
### Figures:
**Diagram (I):**
- Depicts the initial compression \( x_0 \) and the trajectory of the disk up the ramp.
- The disk rolls up, reaching a maximum height \( H \).
**Diagram (II):**
- Depicts the same initial conditions but with the ramp terminating at height \( H/2 \).
- Beyond \( H/2 \), the disk follows a vertical path.
---
Calculating the specifics of the disk's motion involves understanding energy conservation, rotational motion, and potentially projectile dynamics for part (c).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A broomstick (thin rod) has a length of 1.75meters. The broomstick is held vertically with one end in contact with the floor. It is then allowed to fall over, rotating about the end that is in contact with the floor. Calculate the speed of the other end of the broomstick, just before hitting the ground.arrow_forwardA 34.0 kg wheel, essentially a thin hoop with radius 1.60 m, is rotating at 111 rev/min. It must be brought to a stop in 28.0 s. (a) How much work must be done to stop it? (b) What is the required average power? Give absolute values for both parts.arrow_forwardIn the figure here, a solid brass ball of mass 0.252 g will roll smoothly along a loop-the-loop track when released from rest along the straight section. The circular loop has radius R = 0.12 m, and the ball has radius r << R. (a) What is h if the ball is on the verge of leaving the track when it reaches the top of the loop? (b) If the ball is released at height h = 4R, what is the magnitude of the horizontal force component acting on the ball at point Q? (a) h= i 0.30 (b) F = i 0.0148 R 12 m Narrow_forward
- 166. A physics experiment is set up using two pulleys, a string, and a weight as shown below. The larger pulley has a radius of 20 centimeters, and the smaller pulley has a radius of 5 centimeters. The distance between the centers of the pulleys is 51 centimeters. The string is pulled tightly across both pulleys so that AB is a common tangent of the pulleys. Find the length of string from A to B to the nearest tenth of a centimeter. B weightarrow_forwardA hoop of radius Rμ and mass mч and a solid cylinder of radius Rc and mass mc are released simultaneously at the top of a plane ramp of length L inclined at angle 0 above the horizontal plane. Which reaches the bottom of the plane first, and what is the speed of each? (solid cylinder)arrow_forwardIn the figure here, a solid brass ball of mass 0.237 g will roll smoothly along a loop-the-loop track when released from rest along the straight section. The circular loop has radius R = 0.17 m, and the ball has radius r << R. (a) What is h if the ball is on the verge of leaving the track when it reaches the top of the loop? (b) If the ball is released at height h = 7R, what is the magnitude of the horizontal force component acting on the ball at point Q? (a) h= i (b) F= i R g < <arrow_forward
- A spring with spring constant k and equilibrium length zero is attached tothe top of a frictionless hoop of radius R. The spring is stretched and connected to a bead of mass m at the bottom of the hoop. At t = 0 the bead is given an initial speed v0 and the bead moves up the hoop. Find the speed of the bead as a function of position on hoop v(θ).arrow_forwardA vertical spring stretches by 0.15 m to its new equilibrium length when a 3.0 N weight is attached. What is the spring constant?arrow_forwardA mass m = 77 kg slides on a frictionless track that has a drop, followed by a loop-the-loop with radius R = 19.9 m and finally a flat straight section at the same height as the center of the loop (19.9 m off the ground). Since the mass would not make it around the loop if released from the height of the top of the loop (do you know why?) it must be released above the top of the loop-the-loop height. (Assume the mass never leaves the smooth track at any point on its path.) ) What is the minimum speed the block must have at the top of the loop to make it around the loop-the-loop without leaving the track? m/s What height above the ground must the mass begin to make it around the loop-the-loop? m If the mass has just enough speed to make it around the loop without leaving the track, what will its speed be at the bottom of the loop? m/s If the mass has just enough speed to make it around the loop without leaving the track, what is its speed at the…arrow_forward
- Using the definition of dot product: Ax B= (A,B₂ - A₂By)i + (A₂Bx − AxB₂)j + (AxBy - Ay Bx)k Find the cross product Ax B the following vectors: (a) U A = 11 + 3) + 0k B = 3î + 1ĵ + 0k A = 11 - 3j+2k B = -31 + 1ĵ+ 0k (b) (d) A = 1î + 1ĵ + Ok B = 2î - 3j+0k A = 21-5j-1k B = 3î + 1ĵ+ 3karrow_forwardConsider the rotational kinematic motion profile indicated below. t: 0 → 5 s = 0 deg/s , R O(0) = 0 deg = 0 deg/s Y(0) = 0 deg = 6 deg/s , Q Ф(0) = 0 deg O deg %3D t: 5 → 15 s P = 0 deg/s Ó = 6 deg/s Ý(t) = 3/cos(0(t)) deg/s Compute roll angle O at t = 15 s.arrow_forwardA ball of mass 2.3 kg, at one end of a string of length L=4.5 m, rotates in a vertical circle just fast enough to prevent the string from going slack at the top of the circle. Assuming mechanical energy is conserved, the speed of the ball (in m/s) at the bottom of the circle is: m a. 10.50 Ob. 8.13 Oc. 9.39 Od. 14.85 Oe. 6.64arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON