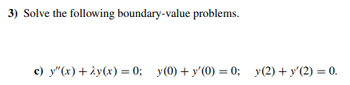
3) Solve the following boundary-value problems. c) y"(x) + 2y(x) = 0; y(0)+y'(0) = 0; y(2) + y'(2) = 0.

Use p(x) = In(x² + x + 7) to answer the questions below. (a) Find p'(x) - (b) Find the equation of the tangent line to p(x) at x = 0. Use y as the dependent variable. (c) If the equation of the tangent line produces an underestimate for values of p(x) near x = 0, which of the following must be true near x=0? Op'(x) is decreasing and p "(x) is positive Op'(x) is decreasing and p "(x) is negative Op'(x) is increasing and p "(x) is positive Op'(x) is increasing and p "(x) is negative

If y(x) satisfies y′′(x)=y′(x)(1−y′(x)),y′(0)=13,y(0)=1, then y(x)=?

1) Please show work

(a) Find P'(2) where P(x)= (x6+3)F(x).   (b) Find Q'(7) where Q(x)= (-6+3G(x))/(x2-8x)