
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Only b-d
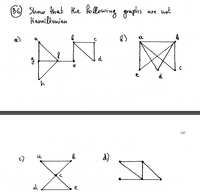
Transcribed Image Text:## Problem 36: Show that the Following Graphs are not Hamiltonian
**Graph (a):**
- Vertices: \(a, b, c, d, e, f, g, h\)
- Structure: The graph is composed of two triangles linked together by a common vertex \(f\). Triangle one includes vertices \(a, f, g, h\), and the second triangle includes vertices \(b, f, e\). The vertex \(b\) is connected to vertex \(c\) which connects to vertex \(d\).
- Explanation: Involves assessing each edge and vertex path to determine the impossibility of a Hamiltonian cycle, where each vertex is visited once without repetition.
**Graph (b):**
- Vertices: \(a, b, c, d, e\)
- Structure: A complete bipartite graph represented in a quadrilateral layout. Includes diagonals intersecting between nonadjacent vertices.
- Explanation: Analyze edge connections and intersections to illustrate that retracing steps is unavoidable, which precludes a Hamiltonian cycle.
**Graph (c):**
- Vertices: \(a, b, c, d, e\)
- Structure: The graph is a bow-tie shape or hourglass structure with overlapping edges at vertex \(c\). The upper part connects vertices \(a\) and \(b\) to \(c\), and the lower part connects vertices \(d\) and \(e\) to \(c\).
- Explanation: Checking possible routes, there’s necessary repetition of the intersection point resulting in no Hamiltonian cycle.
**Graph (d):**
- Vertices: Not labeled
- Structure: Two disconnected figures composed of triangles. The left shape has three points linked, one isolated from the right triangle shape.
- Explanation: As the graph is disconnected, it inherently cannot have a Hamiltonian cycle, as all vertices cannot be visited in a continuous path.
Each graph demonstrates the necessary characteristics to be non-Hamiltonian by either containing disconnections, intersections voiding unique paths, or vertex repetitions—characteristics precluding a Hamiltonian cycle.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

