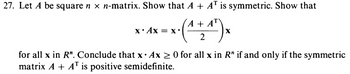
27. Let A be square n x n-matrix. Show that A + AT is symmetric. Show that A+ ATY X. Ax = x X for all x in R". Conclude that x Ax ≥ 0 for all x in R" if and only if the symmetric matrix A + AT is positive semidefinite.

Please send proof of theorem.... Should short and Authentic....

5. For each of the statements given below decide if it is true or false. If it is true explain why. If it is false give a counterexample. a) If A, B are matrices such that AB is defined and is a square matrix (i.e. it has the same number of rows and columns) then BA is also defined. b) If A is an 2 x 2 matrix such that Av = 0 for some non-zero vector v € R² then A cannot be invertible. c) If {V₁, V₂} is a linearly independent set of vectors in R2 and T: R² →→>> R² is a linear transformation then the set {T(v₁), T(v₂)} must be also linearly independent. d) If u, v, w are vectors in R² such that u is in Span(v, w) then v must be in Span(u, w).

20. Suppose that A is a square matrix and suppose that there is another matrix B such that A = BTB. (a) Show that A is positive semidefinite. (b) Show that if B has full column rank (that is, the rank of B is equal to the number of columns of B), then A is positive definite. (Hint: Recall that y· BTx = (By) • x for all x, y.)