
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
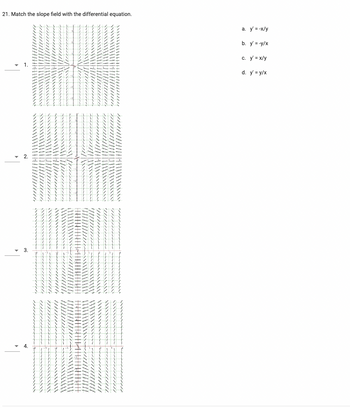
Transcribed Image Text:21. Match the slope field with the differential equation.
3.
4.
NAA
INNAN
SYNT
a. y'= -x/y
b. y'=-y/x
c. y' = x/y
d. y'=y/x
Expert Solution
arrow_forward
Step 1
.
Given differential equation is .
The slope field of is given below
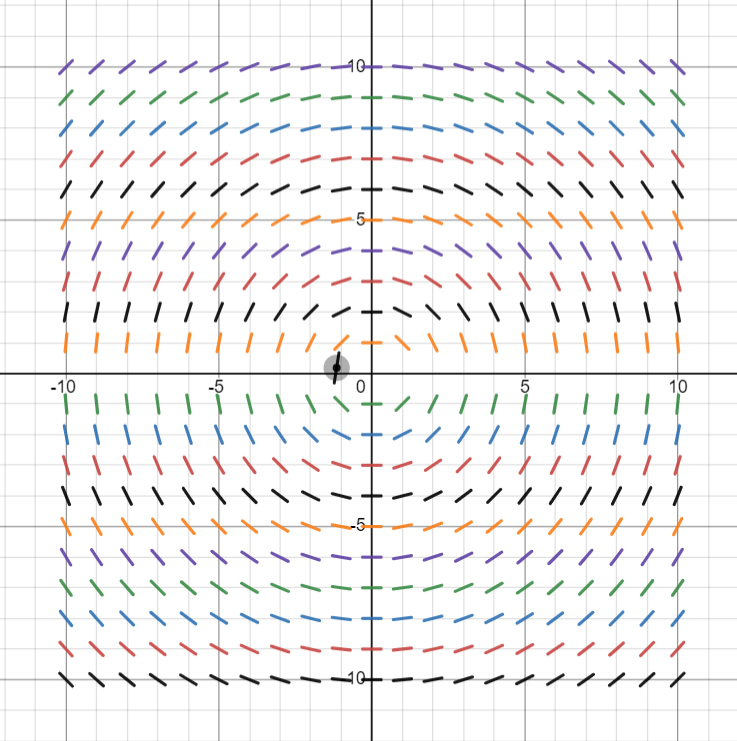
Given differential equation is .
The slope field of is given below.
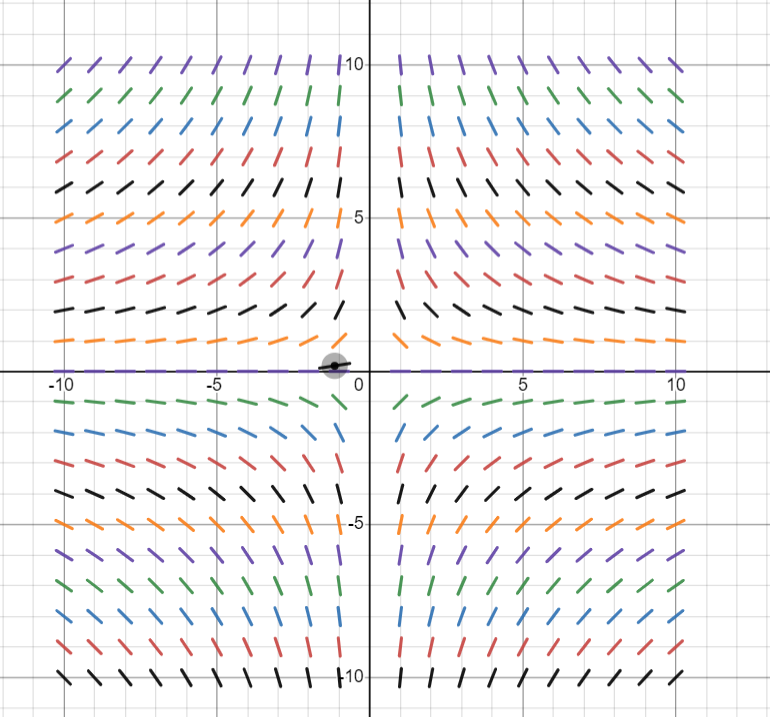
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Similar questions
- Let 13 20 x 20 + y ¹³ = 2 be the equation of a curve in the xy-plane. Find the equation y = T(x) of the tangent line at (1, 1), then evaluate T(21). T(21) = _.arrow_forwardFor y = 1/x^2 , use differentials to approximate the change in y when x changes from 4 to 4.125. Round the answer to two decimal places. (delta)y is approximately:_________arrow_forwardA differentiable function has the value y(2) = 4 and the derivative value y'(2) = -3. Approximate the value of y(2.1). P3 O 3.7 O 3.75 O 3.8 O 3.85 W Jhy 11 12 13 14 15 16 17 18 19arrow_forward
- 9. Explain why the instantaneous rate of change for g(x) = x' cannot be the same for 2 different values of r. 10. Give an example of two functions whose difference represents one of the functions being reiccted in the J-axis. Show that your functions satisfy the conditions.arrow_forwardII. Solve for the following using local linear approximation and differentials 8. Suppose your bank gives an interest rate of 5% that compounds annually. If you currently have Php 100,000.00 in your account (t and the money in your account is given by M = 10 (1.05)', where a the time in years, what is the rate of change of your money after 5 years assuming you do not withdraw or deposit additional mone- from your account? (Just write the expression, no need to write the numerical value). %3Darrow_forward17. If P'(t) is the rate a deer population grows per year, write a sentence explaining what P'(t) dt represents. 18. v(t) = t - 3 is the velocity of a particle in cm/sec. Find the distance traveled by the particle in the first four seconds.arrow_forward
- Find the derivative of the following exponential functions: 1. y = e-4x ans. y' = -4e¬4x 2. y = x?e=* ans. y' = xe-*(2 – x) %3D f (z) = e?(sin z + cos z) ans. f'(z) = 2e² cos z %3D 3.arrow_forwardy=x1.5+1/x2.5 find the derivative. I am getting a solution but I'm unsure of how it is x3.5 at the end result.arrow_forwardx2 2y = y2 + y' =? O A. y' 22 O B. y' = OC. y2 y' O D. y' 81ミarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

