20. + The straight string of a kite makes an angle of elevation from the ground of 60°. The length of the string is 400 feet. What is the best approximation of the height of the kite? A. 200 ft B. 250 ft C. 300 ft D. 350 ft
20. + The straight string of a kite makes an angle of elevation from the ground of 60°. The length of the string is 400 feet. What is the best approximation of the height of the kite? A. 200 ft B. 250 ft C. 300 ft D. 350 ft
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
Related questions
Question
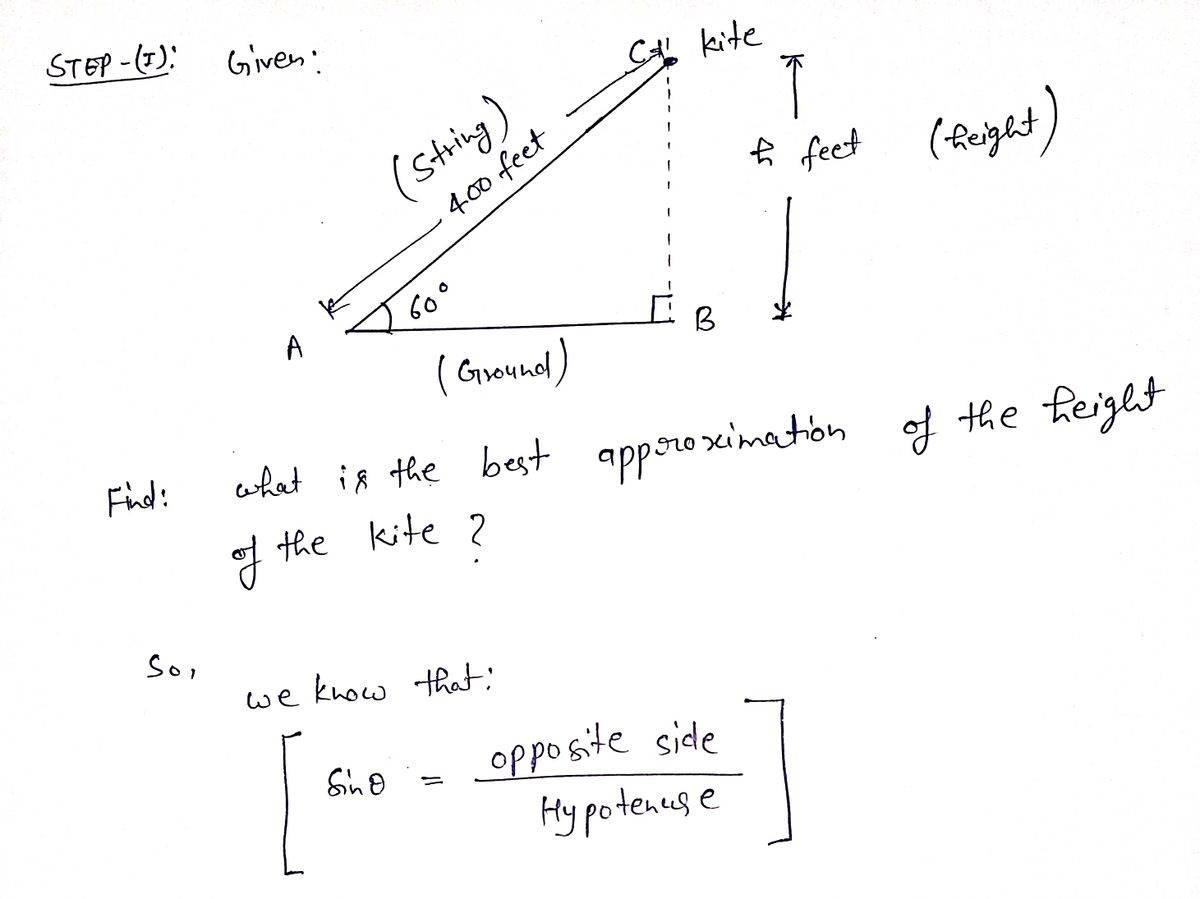
![**Problem 20: Kite Elevation Calculation**
The straight string of a kite makes an angle of elevation from the ground of 60°. The length of the string is 400 feet. What is the best approximation of the height of the kite?
**Options:**
- A. 200 ft
- B. 250 ft
- C. 300 ft
- D. 350 ft
**Explanation:**
To find the height of the kite, we can use trigonometry. Specifically, the sine function relates the angle of elevation to the opposite side (the height of the kite) and the hypotenuse (the length of the string).
\[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \]
Here, \(\theta = 60^\circ\) and the hypotenuse is 400 ft. We want to find the opposite side, which is the height of the kite.
\[ \sin(60^\circ) = \frac{\text{height}}{400} \]
The sine of 60 degrees is \(\sqrt{3}/2\) or approximately 0.866.
\[ 0.866 = \frac{\text{height}}{400} \]
\[ \text{height} = 400 \times 0.866 \approx 346.4 \, \text{ft} \]
Thus, the best approximation of the height of the kite is **350 ft**.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3313e1e9-7cb3-496e-a6fd-03ee912fa280%2F58196e0b-12b2-4393-8e85-41ae3f307cf6%2Fqo826r7_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 20: Kite Elevation Calculation**
The straight string of a kite makes an angle of elevation from the ground of 60°. The length of the string is 400 feet. What is the best approximation of the height of the kite?
**Options:**
- A. 200 ft
- B. 250 ft
- C. 300 ft
- D. 350 ft
**Explanation:**
To find the height of the kite, we can use trigonometry. Specifically, the sine function relates the angle of elevation to the opposite side (the height of the kite) and the hypotenuse (the length of the string).
\[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \]
Here, \(\theta = 60^\circ\) and the hypotenuse is 400 ft. We want to find the opposite side, which is the height of the kite.
\[ \sin(60^\circ) = \frac{\text{height}}{400} \]
The sine of 60 degrees is \(\sqrt{3}/2\) or approximately 0.866.
\[ 0.866 = \frac{\text{height}}{400} \]
\[ \text{height} = 400 \times 0.866 \approx 346.4 \, \text{ft} \]
Thus, the best approximation of the height of the kite is **350 ft**.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images
Similar questions
Recommended textbooks for you
Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,
Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,
Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning