Question

Transcribed Image Text:2. When discussing Bragg scattering we showed that constructive interference between
waves reflecting from Bragg planes occurs when Ar = 2d sin(0) = nλ where Ar was the
path length difference, d was the spacing between Bragg planes, the angle between the
incident motion (light ray or particle direction) and the Bragg plane, n an integer, and λ the
wavelength of the light or deBroglie wave. When discussing the diffraction from a single
crystal of Ni we expressed this condition for constructive interference as D sin(ø) = nλ,
where D was the spacing between Ni atoms, and was the angle between particles shot
perpendicular to a face of the Ni crystal and their reflection to a detector. The relation
Φ
between the angles is: 0 =
and between the distances is d = D sin().
2
(a) Using identity, e¹A
cos(A)
e¹A+e-iA
2
cos(A) + i sin(A), prove that sin(A) =
where i = √-1 is an imaginary number.
=
=
e¹A-e-iA
2i
-
(b) Using the identities from part (a) prove that
sin(A - B) = sin(A) cos(B) – cos(A) sin(B).
-
(c) Using the identities from part (a) prove that sin(A) cos(A)
(d) Returning to the diffraction problem of interest, showing all steps and making use of the
identities derived in parts (b) and (c), show by direct substitution that 2d sin(0) = D sin(o).
and
sin (2A)
2
Expert Solution
arrow_forward
Step 1
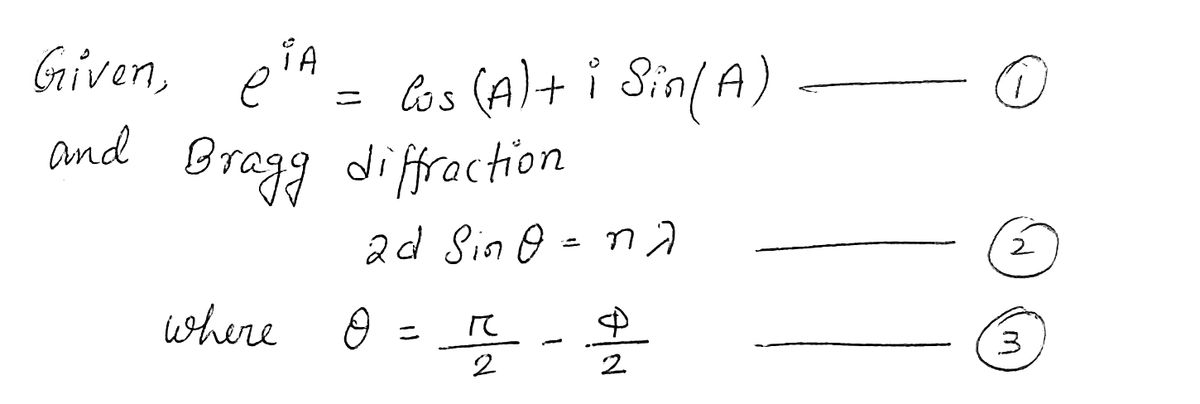
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Electrons with an energy of 0.610 eV are incident on a double slit in which the two slits are separated by 40.0 nm. (a) What is the speed of these electrons? m/s (b) What is the de Broglie wavelength (in nanometers!) of these electrons? nm (c) What is the angle between the two second-order maxima in the resulting interference pattern?arrow_forwardA single beam of electrons shines on a single slit of width 8.7nm. A diffraction pattern (of electrons!) is formed on a screen that is 3.9m away from the slit. The distance between the central bright spot and the first minimum is 5.7cm.What is the kinetic energy (keV, i.e. kilo electron-Volts) of the electrons?Make use of the small angle approximation.arrow_forwardLight of wavelength 327 nm is incident on an uncharged metal sphere of diameter 14.2 cm. If the work function for the metal is 3.68 ev, determine the charge (in C) induced on the sphere due to photoelectric effect. Q = Tutorial Additional Materials Readingarrow_forward
- Calculate the de Broglie wavelength for: a) An electron (9.11 x 10-31) moving at 1 x 106 m/s b) A neutron (1.67 x 10-27 kg) moving at 2.6 x 104 m/s Both particles approach a potential barrier (U = 5 eV) 0.26 nm wide. Calculate the transmittance coefficient for each particle. %3Darrow_forwardLearning Goal: To understand de Broglie waves and the calculation of wave properties. In 1924, Louis de Broglie postulated that particles such as electrons and protons might exhibit wavelike properties. His thinking was guided by the notion that light has both wave and particle characteristics, so he postulated that particles such as electrons and protons would obey the same wavelength-momentum relation as that obeyed by light: \ =h/p, where X is the wavelength, p the momentum, and h Planck's constant. X = 1.06×10-34 Submit Correct m Previous Answers -14 As a comparison, an atomic nucleus has a diameter of around 10 m. Clearly, the wavelength of a moving baseball is too small for you to hope to see diffraction or interference effects during a baseball game. Part C Consider a beam of electrons in a vacuum, passing through a very narrow slit of width 2.00 μm. The electrons then head toward an array of detectors a distance 0.9540 m away. These detectors indicate a diffraction pattern,…arrow_forwardElectrons with an energy of 0.842 eV are incident on a double slit in which the two slits are separated by 40.0 nm. What is the de Broglie wavelength (in nanometers!) of these electrons?arrow_forward
- 2) A thin crystal of the metal oxide with a tetragonal crystal structure and lattice parameters a = 4.05 Å and c = 2.517 Å is tilted so that a 200 kV electron beam travels along the [001] zone axis. Create a schematic diagram of zero order Laue zone (ZOLZ) diffraction pattern for a crystals of thickness: a) 75 Å b) 400 Å You should assume there are no forbidden reflections and that the diffraction intensity drops to zero when the excitation error, s, exceeds the first minimum of the relrod. You should show the approximate number of beams in the ZOLZ circle. (10)arrow_forward1) A laser produces light of wavelength 525 nmnm in an ultrashort pulse. What is the minimum duration of the pulse if the minimum uncertainty in the energy of the photons is 1.0%%? Express your answer with the appropriate units.arrow_forwardX-rays of wavelength 0.0628 nm are scattered from a crystal with a grazing angle of 11.3°. Assume m = 1 for this process. Calculate the spacing between the crystal planes. d = nmarrow_forward
- Learning Goal: To understand how to find the wavelength and diffraction patterns of electrons. An electron beam is incident on a single slit of width a. The electron beam was generated using a potential difference of magnitude V. After passing through the slit, the diffracted electrons are collected on a screen that is a distance L away from the slit. Assume that Vis small enough so that the electrons are nonrelativistic. Ultimately, you will find the width of the central maximum for the diffraction pattern. Part B What is the wavelength of the electron beam? Use the de Broglie relation and the momentum that you found in Part A. Express your answer in terms of h, me, e, and V. X = [5] ΑΣΦ Submit Request Answer ?arrow_forwardLight displays interference patterns, but this is not possible for electrons. True Falsearrow_forward
arrow_back_ios
arrow_forward_ios