
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
![### Joint Probability Density Function of Continuous Random Variables
The continuous random variables \( X \) and \( Y \) have a known joint probability density function \( f_{XY}(x, y) \) given by:
\[
f_{XY}(x, y) =
\begin{cases}
\frac{c \cdot x}{y + 1} & \text{if } 0 \leq y \leq x \leq 1 \\
0 & \text{otherwise}
\end{cases}
\]
where \( c \) is a positive constant.
#### Tasks:
a) **Determine the value of the constant \( c \):**
Find \( c \) such that the function becomes a valid joint probability density function.
b) **Marginal Probability Density Function \( f_X(x) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( X \).
c) **Marginal Probability Density Function \( f_Y(y) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( Y \).
d) **Verification of Functions:**
Verify the results of parts (b) and (c) to ensure that the two probability density functions are valid.
e) **Statistical Independence:**
Determine whether the two random variables are statistically independent.
f) **Expected Value \( E\{XY\} \):**
Obtain the expected value of the product \( XY \).](https://content.bartleby.com/qna-images/question/9328926a-b343-4d47-8a00-cbd9e6e36ac2/afd82448-f5db-488f-82fa-4da35c6511b1/5einod6_thumbnail.jpeg)
Transcribed Image Text:### Joint Probability Density Function of Continuous Random Variables
The continuous random variables \( X \) and \( Y \) have a known joint probability density function \( f_{XY}(x, y) \) given by:
\[
f_{XY}(x, y) =
\begin{cases}
\frac{c \cdot x}{y + 1} & \text{if } 0 \leq y \leq x \leq 1 \\
0 & \text{otherwise}
\end{cases}
\]
where \( c \) is a positive constant.
#### Tasks:
a) **Determine the value of the constant \( c \):**
Find \( c \) such that the function becomes a valid joint probability density function.
b) **Marginal Probability Density Function \( f_X(x) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( X \).
c) **Marginal Probability Density Function \( f_Y(y) \):**
Using the result from part (a), obtain the marginal probability density function of the random variable \( Y \).
d) **Verification of Functions:**
Verify the results of parts (b) and (c) to ensure that the two probability density functions are valid.
e) **Statistical Independence:**
Determine whether the two random variables are statistically independent.
f) **Expected Value \( E\{XY\} \):**
Obtain the expected value of the product \( XY \).
Expert Solution
arrow_forward
Step 1: Continuous probability distribution
As per the guidelines of the Bartleby, solution of only first 3 parts are given.
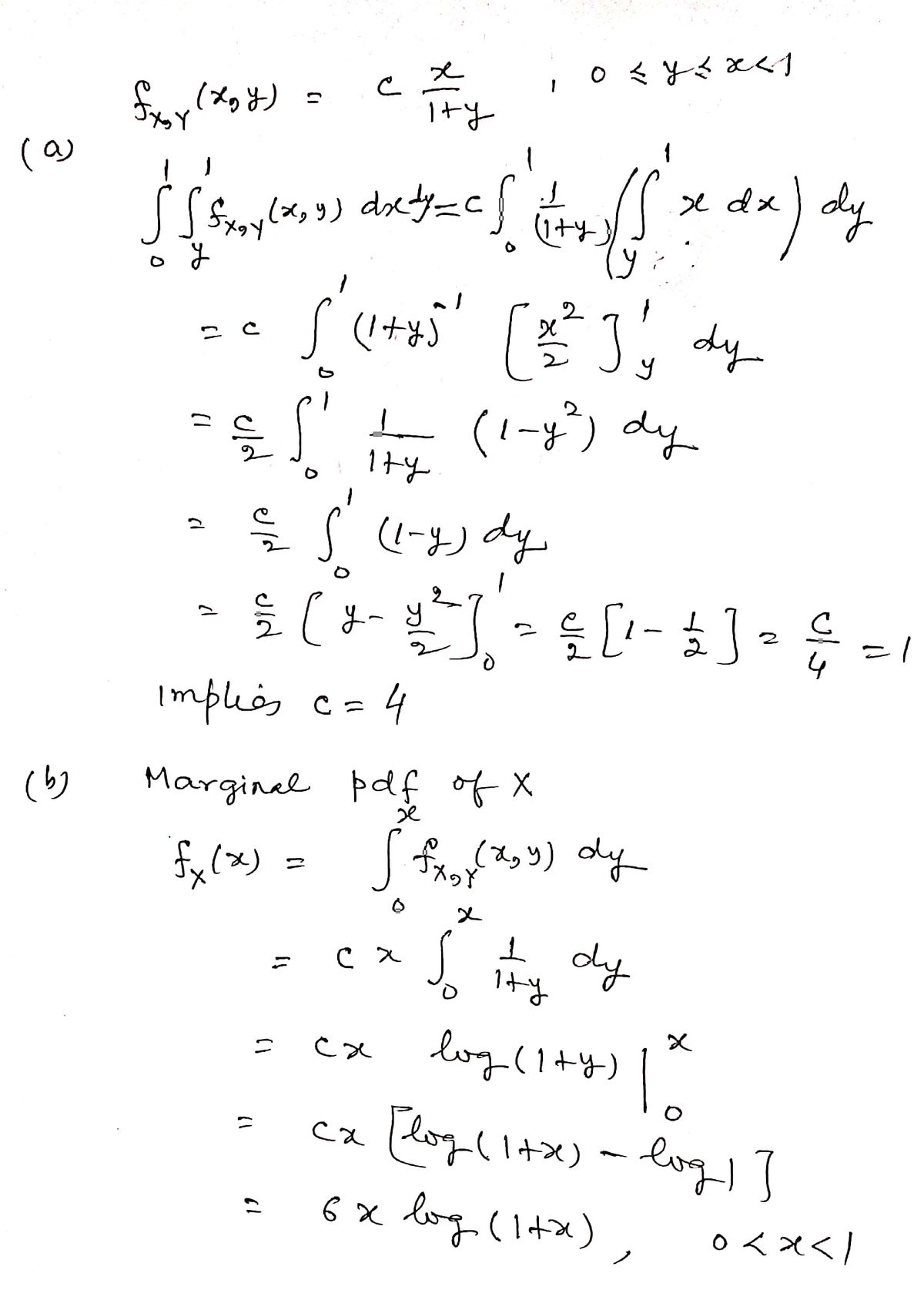
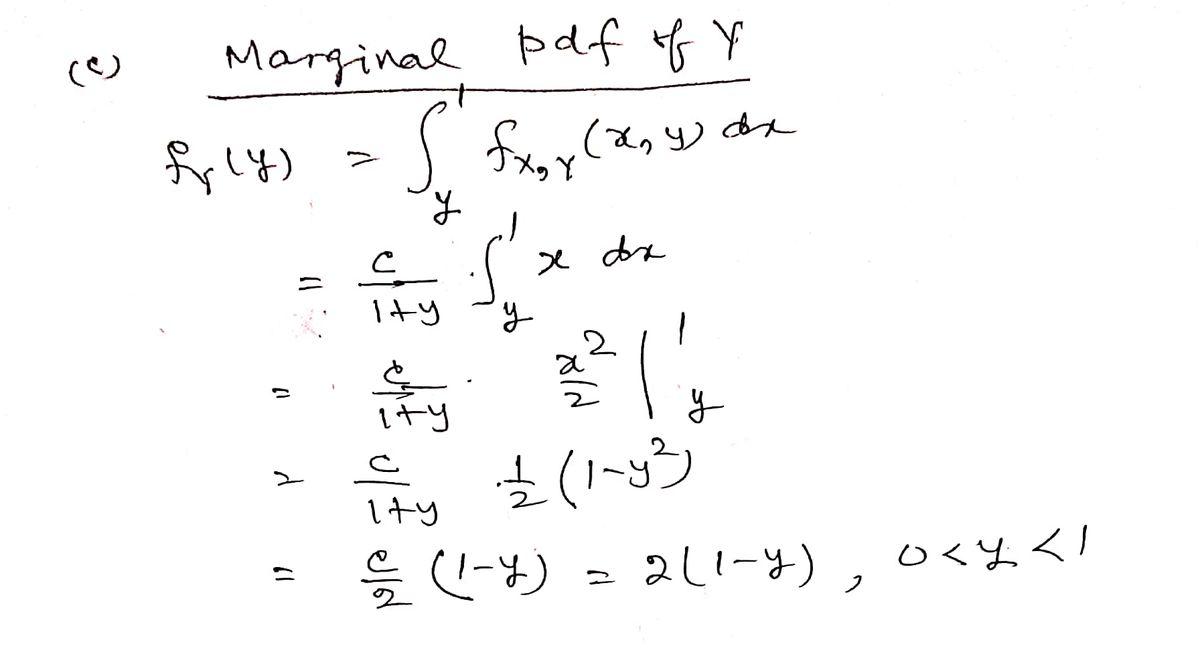
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
