
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
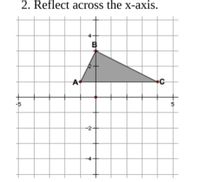
Transcribed Image Text:**Reflect Across the x-axis**
The given diagram shows a triangle on a coordinate grid. The triangle is labeled with vertices A, B, and C. The coordinates for each point are approximately as follows:
- Point A is at (-3, 0)
- Point B is at (-2, 3)
- Point C is at (3, 1)
The grid is divided into equal squares with the x-axis and y-axis intersecting at the origin (0,0). The scales on the axes are consistent, with each square representing one unit.
To reflect this triangle across the x-axis, follow these steps:
1. **Identify the reflection rule**: When reflecting a point (x, y) across the x-axis, its image will be at (x, -y).
2. **Apply the rule to each vertex**:
- Reflect A: (-3, 0) remains (-3, 0) since it lies on the x-axis.
- Reflect B: (-2, 3) becomes (-2, -3).
- Reflect C: (3, 1) becomes (3, -1).
3. **Plot the reflected points**: Once the new positions of A, B, and C are calculated, plot them on the coordinate plane.
4. **Draw the reflected triangle**: Connect the reflected points to form the reflected triangle, which mirrors the original triangle across the x-axis.
The reflection will result in a triangle that is an exact mirror image of the original triangle, across the x-axis.
Expert Solution
arrow_forward
Step 1
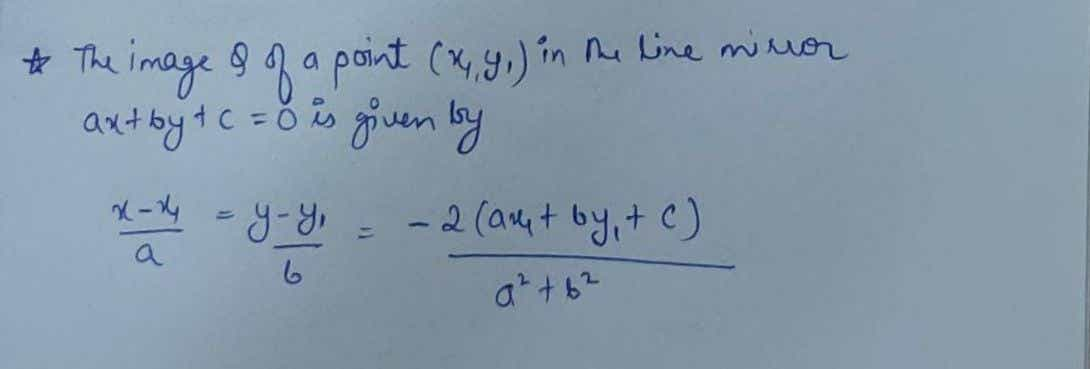
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- Determine the y-intercept of the following. 3 y = -х- 0.2 The y-intercept is. (Type an ordered pair, using integers or decimals.)arrow_forwardFind the function Y=0x +bx+ C Whose graph.contains the Points ,D, €3,-9), 6,27 Solltionarrow_forwardState the x-intercept of the line attached in the coordinate plane.arrow_forward
- What is an equation of the line that passes through the point (1, – 7) and is parallel to the line 3x+ y = 3? | Answer: Submit Answerarrow_forwardA (6,−7) B (2,3)Step 1 of 2 : Plot the given points on the graph. AnswerTo plot a point on the graph, click on the appropriate position on the graph. To move a point, drag the point from its original position to its new position. Points can be moved by dragging or using the arrow keys.arrow_forwardGraph the line. y=-3x-3 MEXI -8 -6 -8 田arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning