
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
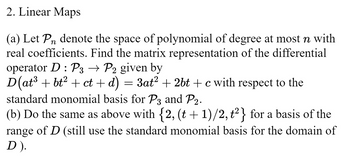
Transcribed Image Text:2. Linear Maps
(a) Let Pn denote the space of polynomial of degree at most n with
real coefficients. Find the matrix representation of the differential
operator D : P3 → P2 given by
D(at³ + bt² + ct + d) = 3at² + 2bt + c with respect to the
standard monomial basis for P3 and P2.
(b) Do the same as above with {2, (t + 1)/2, t²} for a basis of the
range of D (still use the standard monomial basis for the domain of
D ).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Can The solver please include hand written steps and all matrix notation possible? Thank you!arrow_forward-9 V₁ = --[-] and X₂ such that T(x) is Ax for each x. Let x = A = X₁ -2 [3] and let T: R² R² be a linear transformation that maps x into x₁v₁ +X₂V₂. Find a matrix A -8 and V₂ =arrow_forwardUsing linear algebra, show that G={p1(x)=1−x+x^2, p2(x)=x, p3(x)=x+x^2} is a basis of P2, the vector space of polynomials of degree at most two with real coefficients.arrow_forward
- 9. Let and B 3 = {[B]-[-2]} = B' ={[2¹].[6]} be two ordered bases for R². Find the change of basis matrix [I]B'.arrow_forward9. Consider the following 2 x 2 matrix A and basis S of R²: A ¹ = [² %) and 5 = {[_¹₂] · [_³;]} The matrix A defines a linear operator on R². Find a matrix B that represents the mapping A relative to the basis S.arrow_forwardLet L: R3 R2 be defined by the following. X1 + X3 ***] 8x2 Suppose X1 L X₂ P = = 1 -(HH) 4 3 3 1 2 B₁ = 4 ={[8][;}} is an ordered basis for the domain and B₂ = is an ordered basis for the range. Find the matrix representation P for L relative to B₁ and B₂ such that [L(u)]b₂ = P[u]ß₁'arrow_forward
- 7. (a) Consider the ordered basis ß = [1,1 +x, 1 + x + x²] for V = P₂ and F = R. Suppose is in P2 and you know these coordinates: [] = (1, 2, 3). Find the vector 7. (b) Let A be a 2 x 2 matrix and a be a real number. Prove that det (a A)=a² det(A)arrow_forward3. Given A= [1 0 (a) Give the vector c so that Ax = b has a solution if and only if b - c = 0. (b) Give a basis of the subspace of all vectors b such that Ax = b has a solution. %3Darrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

