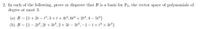
2. In each of the following, prove or disprove that B is a basis for P3, the vector space of polynomials of degree at most 3. (a) B = {1+2t – t3,3 + t+ 4t2, 6t2 + 2t3, 4 – 5t2} (b) B = {1 – 2t2, 2t + 3t, 2+ 3t - 3t2, -1 – t+t2 + 3t}

Which one of the following is not a basis for the vector space consisting of polynomials of degree less or equal to 2?  See attached file.

Can anyone explain why x2 and x3 is a free variable in the third line of the solution?

3. Do the vectors (1, 1,0), (0, 1, 1) and (1,0, –1) form a basis of R3?

a) Find , \pl, d (p, q), and then find the angle between them for the polynomials in P2 if p(x) = -3x² + 2x – 5 , and q(x) = -x+5x? b) Verify that the basis set S = {(3,0,4), (-4,0,3), (0,1,0)} is orthogonal then find the coordinates of the vector u = (-5,5,1) using inner product