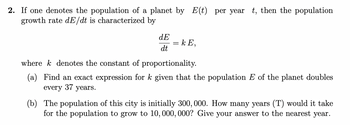
2. If one denotes the population of a planet by E(t) per year t, then the population growth rate dE/dt is characterized by dE dt = kE, where k denotes the constant of proportionality. (a) Find an exact expression for k given that the population E of the planet doubles every 37 years. (b) The population of this city is initially 300, 000. How many years (T) would it take for the population to grow to 10, 000, 000? Give your answer to the nearest year.

Q: Newton's law of cooling says that a hot object cools rapidly when the difference between its…

A:

Q: Radium decomposes at a rate proportional to the amount at any instant. In 100 years, 100 mg of…

A: Radium decomposed proportional to amount dy/dt ∞ y dy/dt =ky dy/y = kdt  Integrate on both sides ∫…

Q: . The daily amount of smog produced by cars coming into a city is given by y = 2 + 0.01x3/2, where y…

A:

Q: a new substance C is to be formed by removing two units from each of two substances whose initial…

A: 1st we will formed a differential equation for amount of C and then solve it to get actual amount of…

Q: If a quantity grows/decays at a rate proportional to its size, its growth can be expressed as dQ/dt…

A:

Q: Suppose that a room containing 1000 cubic feet of air is originally free of carbon monoxide (CO).…

A: Given Information:The room contains 1000 cubic feet of carbon monoxide. Initially, cigarette smoke…

Q: 3. In an experiment, the growth rate of a population of bacteria t hours after the bacteria are…

A:

Q: Suppose w(t) represents the weight of a patient, in pounds, t years after an office visit. (a)…

A: For (a),         We need to interpret ∫01w'(t)dt=-10 in terms of weight and time. Now,…

Q: A room with a volume of 5000 ft3 is full of air which contains 2% (CO). Pure air containing no (CO)…

A: Given that: Volume = 5000 ft3 Let x(t) denotes the amount of CO in the room at time t. The room…

Q: Initially 100 milligrams of a radioactive substance was present. After 6 hours the mass had…

A:

Q: (a) In a certain culture of bacteria the rate of increase is proportional to the number present. (i)…

A: Since you have posted a multiple question ,I will solve the first question  for you. To get…

Q: The motion of an particle follows an exponential function s(t)=et. (a) Determine the velocity of the…

A: If the distance function is differentiated with respect to the time, then the velocity function is…

Q: Under certain conditions, cane sugar with water is converted into dextrose at a rate which is…

A: We need to find out the amount converted un 1.5 hours. in grams,

Q: The population of mosquitoes in a certain area increases at a rate proportional to the current…

A:

Q: The period T of a pendulum is determined by T = 27 with L the length of the pendulum and g the…

A:

Q: 1.) (Sections 4.1 & 4.2) A virus is spreading through a population, with 8% more people actively…

A: topic - exponential function

Q: The initial mass of a certain species of fish is 3 million tons. The mass of fish, if left alone,…

A: Solve the given problem