Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
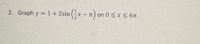
Transcribed Image Text:**Problem 2: Graphing a Sine Function**
Graph the function \( y = 1 + 2\sin\left(\frac{1}{2}x - \pi\right) \) over the interval \( 0 \leq x \leq 6\pi \).
**Function Analysis:**
1. **Transformation Basics:**
- The function is a transformed sine wave.
- The amplitude of the standard sine function is modified by a factor of 2, which means the graph will vertically stretch by 2.
- There is a vertical shift up by 1 unit, which affects the midline of the graph.
- The phase shift is determined by the \(- \pi\) inside the sine function, translating the graph to the right by \(\pi\) units.
- The horizontal dilation is caused by the \(\frac{1}{2}\) within the function, which increases the period of the sine wave.
2. **Period and Phase:**
- The standard period of \( \sin(x) \) is \( 2\pi \).
- For \( \frac{1}{2}x \), the period is \(\frac{2\pi}{\frac{1}{2}} = 4\pi\).
- Thus, every cycle of the sine wave completes over \( 4\pi \).
3. **Graph Details:**
- Start plotting at \( x = \pi \) due to the phase shift.
- The maximum point of the graph will be at \( y = 3 \) (1 + amplitude of 2), and the minimum point will be at \( y = -1 \) (1 - amplitude of 2).
- The midline of the wave is at \( y = 1 \).
These details will help in understanding the graphical representation of the given function over the specified interval.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- how continuity is destroyed at x=c for each grapharrow_forwardConsider the four graphs shown below. Select all graphs that satisfy the following four conditions: • f"(x) 0 when x 3, • f(-1) = -3, and . • f(1) = -1. 0 14 -20 -4 -4 -2 f(x) 2 0 -7 -4 -64 4, f(x) 41 f(x) 2 -2 W √2+ -44 -64 -8+ 4 2 4 2 X X X f(x) -2 0 2 4 W -2 Xarrow_forward9. Let n(x) = -x² + 4x-1 (a) Write n(x) in vertex form. (b) Sketch the graph of n(x).arrow_forward
- Compare the graph of n = +x). 1 with n(x) =x². 1 n = 6) - 1 shifts left 36 units, shifts upward 1 units, and shrinks by a factor of 9 n = 1 shifts left 6 units, shifts downward 1 units, and shrinks by a factor of 81 x+ 6)| – 1 shifts right 36 units, shifts upward 1 units, and shrinks by a factor of 81 1 - 1 shifts right 6 units, shifts downward 1 units, and shrinks by a factor of 81 N = 1 (x+ 6) 1 shifts right 6 units, shifts upward 1 units, and shrinks by a factor of N = 81arrow_forward5. Write y 3(x- 5)(x-6) in standard form and graph y 3(x-5)(x-6) 3x-33x+90 c. y= a. y= 3x -11x+ 30 10 10 10 x io 10 x 10 40 b. y 3x-11x+ 30 d. y = 3x - 33x + 90 10 1:10 xarrow_forwardx2 1. Graph f(x)=-: x+1arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning