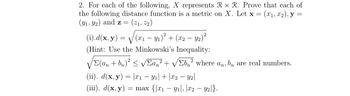
2. For each of the following, X represents Rx R. Prove that each of the following distance function is a metric on X. Let x = (₁, ₂), y (91, 92) and z = (21, 22) (i).d(x, y) = √(x1 - y₁)² + (x2 - y₂)² (Hint: Use the Minkowski's Inequality: √Σ(an + bn)² ≤ √Σan² + √b² where an, bn are real numbers. (ii). d(x, y) = x₁y₁| + x2 - y2| (iii). d(x, y): = max {x₁y₁, x2 - y2|}.

2. For each of the following, X represents Rx R. Prove that each of the following distance function is a metric on X. Let x = (x₁, x₂), y = (91, 92) and z (21, 22) = (i).d(x, y) = √(x₁ - y₁)² + (x2 − y2)² (Hint: Use the Minkowski's Inequality: Σ(an + bn)² ≤ √Σan² + √b² where an, bn are real numbers. (ii). d(x, y) = (iii). d(x, y) = max {x1y₁, x2 - y2|}. - x₁y₁| + x2 - y₂| - 3. Extend each of the above three distance functions to define on XR and show that in each case the distance function is a metric.

Please solve number 3

2. Use Fermat's Method of Adequality to find subtangent of the function f(x) = x³ at the point (2,8). Then use the subtangent, similar triangles, and the Pythagorean Theorem to find the normal and subnormal and the slope of the tangent line at the same point. So, you need to find four things: the subtangent, normal, subnormal, and slope of the tangent line. Do not approximate with decimals.