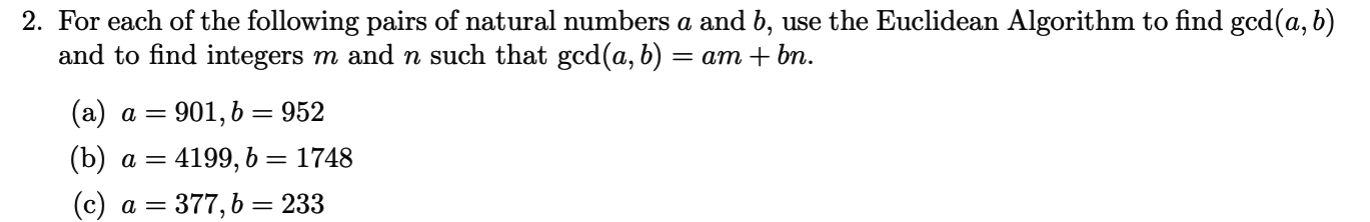
2. For each of the following pairs of natural numbers a and b, use the Euclidean Algorithm to find gcd(a, b) and to find integers m and n such that gcd(a, b) = am + bn. (a) a = 901, 6 = 952 = 4199, 6 = 1748 (b) a (c) a = 377, b = 233

Use the Euclidean algorithm to obtain integers x, y and z satisfying the following (198, 283, 512) (56, 72) Find the [3799, 7337] Find all the positive integer number d such that 18|d and d]216 kindly ..solve both Questions

Discrete Math

(mod 11) 11b = 1. Find all solutions 0 < r < 11 to 23r+r¹¹ = 2 Use the Euclidean Algorithm to find a, b € Z so that 57a+

Prove the theorem of division algorithm - If a and b are integers such that b>0, then there are unique integers q and r such that a=bq+r with 0sr< b.

Ifa = 282 and b = 34 then find the following 1) Find ged(a, b) "use Euclidean algorithm" 2) Write the gcd(a, b) as a linear combination of a and b 3) Write a and b in standard form of prime factorization 4) Find L.c.m(a,b)

Using Euclid's algorithm, solve the following

(a) For integers a, b, q, r, prove that if a = bq + r then (a, b) = (b, r). (b) Determine (1000, 2025) by using the Euclidean algorithm. Then express the answer as a linear combination of 1000 and 2025. Show all your working. (c) Suppose that G = (a), a ‡e, and a5 : = e. Construct a Cayley table for the group (G,.). (d) Determine the right cosets of ((1 2), [1]) € S3 × Zi₂. (e) Find the subgroups of Z24.

1. For each pair of integers m and n, use the division algorithm to divide m by n. Write the result in the form m = q⋅n + r where 0 < r < n. a. m = 32 and n = 9 b. m 62 and n = 7 = c. m -45 and n = 11 d. m 3 and n = 8 2. For each pair of integers a and b, use the Euclidean Algorithm to find the GCD(a, b). Then use Theorem 92 to find the LCM(a, b) a. a = 48 and b = 54 b. a = 330 and b = 156 c. a=1188 and b = 385 3. For each pair of integers m and d, calculate m mod d. Show your work! a. m 43 and d = 9 b. m 50 and d = 7 c. m 28 and d = 5 d. m = 30 and d = 2

3. If a = 99 and b = 374. Use the Euclidean algorithm to find the gcd(a, b) and compute integers x and y for which ах + by 3 gcd(а, b).