Question
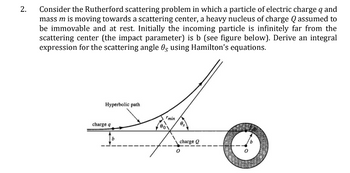
Transcribed Image Text:2. Consider the Rutherford scattering problem in which a particle of electric charge q and
mass m is moving towards a scattering center, a heavy nucleus of charge Q assumed to
be immovable and at rest. Initially the incoming particle is infinitely far from the
scattering center (the impact parameter) is b (see figure below). Derive an integral
expression for the scattering angle 0, using Hamilton's equations.
Hyperbolic path
charge q
min
charge Q
0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- A charged sphere has charge density p=p,r sin(p) Find the total charge in the sphere. Note phi is the angle to the zaxis, remember some textbooks use theta for the angle from the zaxis and phi in the xy plane.arrow_forwardConsider the special shape pictured in the diagram below. It is a cylinder, centered on the origin with its axis oriented along z, and it has been partially hollowed to leave two cone-shaped cavities at the top and bottom of the cylinder. The radius of the object is a, its height is 2a, and the solid part of the object (the shaded region that is visible in the rightmost panel of the illustration above, which shows a drawing of the cross-section of the object) has a uniform volume charge density of po. Assume that the object is spinning counter clockwise about its cylinder axis at an angular frequency of w. Which of the following operations is part of the calculation of the magnitude of the current density that is associated with the motion of the rotating object as a function of r (select all that apply)?arrow_forwardAn insulating sphere of radius a has a non-uniform volume charge density p = 4 where A is a constant and r is the spherical radial coordinate. This insulating sphere is surrounded by a concentric conducting spherical shell of inner and outer radii b and e, respectively (b>a) as shown in the figure. What are the induced surface charge densities on the inner (oinner) and outer (đouter) surfaces of the condueting shell? Select one: Aa Aa Oouter = Oinner = Aa dinner = Aa Oouter = - O'inner = -47Aa², 47 Aa? Oouter = 47 Aa 4 Aa Oinner = Jouter = b2 Ab Ac Oouter = Oinner = a² °arrow_forward
- Consider a spherical metal shell of inner radius ?. A point charge ? = −5 mC is located at a distance ?/2 from the centre of the shell. The shell is neutral. a) Calculate the induced charge on its outer surface. b) Sketch the charge distribution at the inner and the outer surfaces of the shell, and the E-field lines inside and outside the metal shell.arrow_forward113 In the case of scattering from a spherically symmetric charge distribution, the form factor is given by sin (4) qr/h F(q²) = √p(r) ³ -4л r²dr where p(r) is the normalized charge distribution. (a) If the charge distribution of proton is approximated by p(r) = A exp(-r/a), where A is a constant and a is some characteristic "radius" of the proton. Show that the form factor is proportional to (1+2) where 90 is h/a. (b) If q = 0.71 (Gev) ². determine the characteristic radius of the proton.arrow_forwardhelparrow_forward
arrow_back_ios
arrow_forward_ios