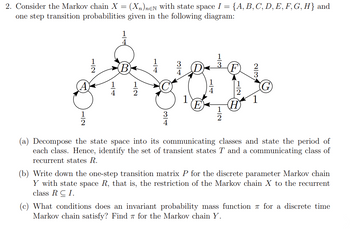
2. Consider the Markov chain X = (Xn)neN with state space I = = {A, B, C, D, E, F, G, H} andone step transition probabilities given in the following diagram:1534(0)A71WIN(a) Decompose the state space into its communicating classes and state the period ofeach class. Hence, identify the set of transient states T and a communicating class ofrecurrent states R.(b) Write down the one-step transition matrix P for the discrete parameter Markov chainY with state space R, that is, the restriction of the Markov chain X to the recurrentclass RCI.(c) What conditions does an invariant probability mass function for a discrete timeMarkov chain satisfy? Find for the Markov chain Y. (d) Stating any general results that you appeal to, deduce the following:i. Y is positive recurrent,ii. the distribution of Y after it has been running for a very long time,iii. the long-term proportion of time spent in each of the states,iv. the average time, ET;, for Y to first return to each state i,v. the long-term average value of f(X₂), where ƒ : I → R is a function with f(A)ƒ(B) = 2, ƒ(C) = 3, ƒ (D) = 4, ƒ (E) = 5, ƒ (F) = ƒ(G) = f(H) = 6,= 1.vi. starting initially in state B, what is the average number of visits made to state Cbefore first returning to B.

“Since you have posted a question with multiple sub-parts, we will solve the first three sub-parts…

Answered: 2. Consider the Markov chain X =…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

7. The following 4-state Markov model with constant intensities a, B and y is used to model a pension scheme for male members aged 55. Age is defined as age last birthday on January 1". The states are w: Active, a: Preserved Benefit, b: Drawing pension and d: Dead. The following data were collected over an observation period covering a single calendar year on 1000 male members of the above pension scheme, all of whom are aged 55: Total waiting time in state w: 800 years Total number of transfers from state w to state a: 200 Total number of transfers from state w to state b: 200 Total number of transfers from state w to state c: 20 Find the likelihood function L(a, B.y) for these data and hence find the maximum likelihood estimates of a,ß and y.
Consider the Markov chain with state space S = {0, 1, 2,...} and transition probabili- ties Poo = 1 - P. P02 = P, and Pr,x+2= P₁ P2,2-1=1-p, for x = 1,2,... For which values of p is this a transient chain?
For the attached transition probability matrix for a Markov chain with {Xn ; n = 0, 1, 2,.........}: a) How many classes exist, and which two states are the absorption states? b) What is the limn->inf P{Xn = 3 | X0 = 3}? b) What is the limn->inf P{Xn = 1 | X0 = 3}?
1. For each of the transition matrices given below, list absorbing state(s), and determine the period of each of the states in each Markov chain. (a) P = (d) P = 1120 CLI2L 1434L3 0 ܚ . ܟ ܝ. | ܟ ܝܕ . ܚ 0 00 0 0 0 0 0 3I4LI4 LIABI+ 0 0 (b) P = 1 0 Lo (e) P = 0 1 1 0 0 1333 COLITOLIN 0 0 0 0 0 213 100 0 0 3 00 100 0 -0 WIN 1 0 0 0 0 0 0 00 1 0 0 4|012 TWO O 0 0 0 0 0 (c) P = (f) P = 0 1|2 1|3 OLT20IN +15 O N|TN|TO 120 HINO OLI3 O 0 LI5L4L 1113 2I5
40. A Markov Chain with 4 states is currently equally likely to be in states 3 and 2, but is 4 times as likely to be in state 1 as in 3, and is 2 times as likely to be in 4 as in 1. What is the state vector that describes this situation?
Milan.stt
2. Consider a Markov chain {Xn}n≥o having the following transition diagram: 1/2 1 2 5 1/4 3 4 1/2 1/4 6 7 1/2 For this chain, there are two recurrent classes R₁ = {6,7} and R₂ = {1,2,5}, and one transient class R3 = {3,4}. (a) Find the period of state 3. (b) Find f33 and f22. (c) Starting at state 3, find the probability that the chain is absorbed into R₁. (d) Starting at state 3, find the mean absorbation time, i.e., the expected number of steps that the chain is absorbed into R₁ or R₂. Note: there are missing transition probabilities for this chain, but no impact for your solution.
12. Let Z be an irreducible discrete-time Markov chain on a countably infinite state space S, having transition matrix H = (hij) satisfying hii = 0 for all states i, and with stationary distribution v. Construct a continuous-time process X on S for which Z is the imbedded chain, such that X has no stationary distribution.
c) Consider the transition Markov chain with three states S = (1, 2, 3) as shown below. %3D 1 Given that; P(X, = 1) = 3' fine P(X, = 1,X, = 2,X2 = 3) N/3 1/2 1/2 1/4 1/2 1/4
2. For all permissible p values, determine the equivalence classes of the Markov chain with the following transition matrix P, classify states as transient or recurrent, and classify the Markov chain as irreducible or reducible. 0. 1-p 1 - 0. P = 0. 1-p 0. 1-p
Refer to the sample data for pre-employment drug screening shown below. If one of the subjects is randomly selected, what is the probability that the test result is a false positive? Who would suffer from a false positive result? Why? Positive test result Negative test result Drug Use Is Indicated Drug Use Is Not Indicated Subject Uses Drugs 39 14 Subject Is Not a Drug User 2 36 Pre-Employment Drug Screening Results The probability of a false positive test result is (Round to three decimal places as needed.)
A state vector X for a four-state Markov chain is such that the system is three times as likely to be in state 4 as in 3, is not in state 2, and is in state 1 with probability 0.2. Find the state vector X.

SEE MORE QUESTIONS

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS