Question

Transcribed Image Text:2. A block of mass m is moving with speed v along a horizontal surface when it collides
with a uniform rod of mass 2m and length L attached at one end to a pivot. The surface
and pivot have negligible friction. The rod is vertical when the block collides with the end
of the rod. The block sticks to the rod, and the block-rod system rotates so that the end
of the rod reaches a height h, as shown above. The total rotational inertia of the rod
about the pivot is 2mL/3. Express answers in parts (a), (b), and (c) in terms of m, L, v,
and physical constants as appropriate.
2m, L
a. Derive an expression for the angular speed of the block-rod system immediately
after the collision.
b. Show that the change in height h of the bottom of the rod can be given by the
equation A = 3v-/20g.
c. Derive an expression for the mechanical energy dissipated during the collision.
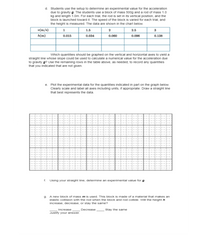
Transcribed Image Text:d. Students use the setup to determine an experimental value for the acceleration
due to gravity g. The students use a block of mass 500g and a rod of mass 1.0
kg and length 1.0m. For each trial, the rod is set in its vertical position, and the
block is launched toward it. The speed of the block is varied for each trial, and
the height is measured. The data are shown in the chart below.
v(m/s)
1.5
2
2.5
3
h(m)
0.015
0.034
0.060
0.096
0.138
Which quantities should be graphed on the vertical and horizontal axes to yield a
straight line whose slope could be used to calculate a numerical value for the acceleration due
to gravity g? Use the remaining rows in the table above, as needed, to record any quantities
that you indicated that are not given.
e. Plot the experimental data for the quantities indicated in part on the graph below.
Clearly scale and label all axes including units, if appropriate. Draw a straight line
that best represents the data.
1 Using your straight line, determine an experimental value for g.
g. A new block of mass m is used. This block is made of a material that makes an
elastic collision with the rod when the block and rod collide. WilIl the height h
increase, decrease, or stay the same?
Increase
Justify your answer.
Decrease
Stay the same
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
I am confused about the solutions
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
I am confused about the solutions
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
- 4. A cylinder with mass m1 = 2.5 kg and radius r = 20 cm rotates counterclockwise about a vertical axis through its center with angular speed @1=5.0 rad/s. A second cylinder with mass m₂ = 1.0 kg and radius r1= 15 cm rotates clockwise about the same axis with angular speed @2 = 12 rad/s. The upper cylinder is lowered onto the lower one and they couple so they have the same rotational axis. Find the angular speed of the combination. Is kinetic energy conserved? If not, what happened to the a) b) kinetic energy? m₂ = 1.0 kg T2 = 15 cm m₁ = 2.5 kg n W₂ = 12 rad/s T₁ = 20 cm w₁ = 5 rad/sarrow_forwardPlease refer to the picture to help answer the questions. A ice skater goes into a spin standing vertically with his arms outstretched horizontally. We can crudely model his torso and legs as a cylinder with radius 0.1m and mass 52 kg and each arm is a rod with mass 4 kg and length 0.9 m. The skater will initially spin at 2.0 rad/s. Question 1: what is the moment of inertia of the skater's torso and legs. Please answer in kg m^2. Question 2: What is the moment of inertia of one of the skater's arms? Please answer in kg m^2. Question 3: What is the total moment of inertia of the skater? Please answer in kg m^2arrow_forwardA disc (thin cylinder) of mass 0.05 kg and radius 0.65 m is rotating on a frictionless axle at a constant rate of 77 RPM. What a the angular velocity and angular momentum of the disc? の = rad/s L = kg-m2 A second disc of 0.02 kg and 0.23 m is dropped down the axle on top. The two then rotate together. What is the final angular velocity and RPM of the system of discs? rad/s RPM = RPMarrow_forward
- A rod of mass 5 kg has a length of 3 m. The rod is fixed at its center but is still free to rotate about its axis (1 = 1/2 ML2). The rod is initially at rest until a piece of putty of mass 1.4 kg strikes one end of the rod at a speed of 6.7 m/s. The putty sticks to the rod and the putty-rod combo begins to rotate. What is the final rotational speed of the putty-rod combo? Please select the correct answer from the choices shown below: ⒸA. 1 rad/s OB. 4 rad/s C. 2 rad/s D. 3 rad/sarrow_forwardJohn McClane, desperately trying to escape the bad guys in an upper floor of a skyscraper, grabs a fire hose and crashes out a window. He falls toward the ground, dragging the hose with him. The hose is wound around a cylinder that has a moment of inertia equal to 5 kg m2, and the hose unspools from the cylinder as McClane falls. Assuming that the hose is pulled from the cylinder at an angle that is perpendicular to the cylinder's radius, what is McClane's acceleration? Let McClane's mass be 75 kg and the radius of the cylinder be 0.5 m. Neglect friction and air resistance. Hose Wall Spool McClanearrow_forward6.arrow_forward
- A light rigid rod of mass 3.00 kg and length 2.00 m rotates about an axis perpendicular to its length and passing through its center as shown in the figure below. Two particles of masses m1 = 6.00 kg and m2 = 3.50 kg are connected to the ends of the rod. What is the angular momentum of the system if the speed of each particle is 4.05 m/s? m2arrow_forwardAn entertainer has perched a 281 g spinning plate on top of a pole. The plate has a radius of 12 cm and is spinning at 68 rpm. A 277 g cup with a moment of inertia of 0.005 kg•m2 is then placed in the center of the plate. The cup beings to spin with the plate. Once the two objects are spinning together, what rate of spin, in revolutions per minute do they have? Answer to one decimal placearrow_forwardThe masses and coordinates of four particles are indicated in the following table. 50 g x - -1.0 cm y = 2.0 cm 30 gx- -2.0 cmy- 0.0 cm 40 gx = 1.0 cm y = -2.0 cm 45 gx = -3.0 cm y = -4.0 cm (a) What is the rotational inertia of this collection about the x axis? g-cm? (b) What is the rotational inertia of this collection about the y axis? | 9-cm? (c) What is the rotational inertia of this collection about the z axis? g.cm2 (d) Suppose the answers to (a) and (b) are A and B, respectively. Then what is the answer to (c) in terms of A and B? AB A + B O (A + B)? O A -B O Oarrow_forward
- Multiple-Concept Example 10 reviews the approach and some of the concepts that are pertinent to this problem. The figure shows a model for the motion of the human forearm in throwing a dart. Because of the force M applied by the triceps muscle, the forearm can rotate about an axis at the elbow joint. Assume that the forearm has the dimensions shown in the figure and a moment of inertia of 0.062 kg-m? (including the effect of the dart) relative to the axis at the elbow. Assume also that the force M acts perpendicular to the forearm. Ignoring the effect of gravity and any frictional forces, determine the magnitude of the force M needed to give the dart a tangential speed of 4.5 m/s in 0.14 s, starting from rest. 0.28 m Axis at elbow joint 0.025 m Number i Unitsarrow_forwardA 0.45 kg tetherball is attached to a pole and rotating in a horizontal circle of radius r₁ = 1.4 m and is circling at angular speed = 1.42 rad/s. As the rope wraps around the pole the radius of the circle shortens and became r2 = 0.9 m, that decreases the moment of inertia of the rotating tetherball. What is the moment of inertia of the rotating ball before the rope is wrapped around the pole measured in kgm² (answer with 3 decimal places)?arrow_forwardA uniform thin rod ( ML2) of length 0.9 m and mass 2.4 kg can rotate in a horizontal plane about a vertical axis through its center. The rod is at rest when a 4.3 g bullet traveling in the rotation plane is fired into one end of the rod. The bullet's path makes angle e = 60° with the rod. If the bullet buried in the rod and the angular velocity of the rod is 10 rad/s immediately after the collision, what is the bullet's speed (in m/s) just before impact? Axisarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios