
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
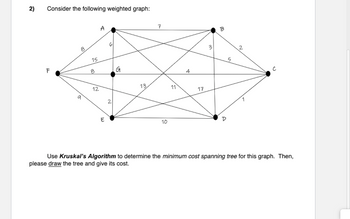
Transcribed Image Text:### Problem 2: Weighted Graph Analysis
**Task:** Consider the following weighted graph.
**Graph Details:**
- **Vertices:** There are six vertices in the graph, labeled A, B, C, D, E, and F.
- **Edges and Weights:**
- A to B: 7
- A to C: 6
- A to D: 8
- A to E: 9
- A to F: 8
- B to C: 2
- B to D: 1
- B to E: 3
- B to F: 7
- C to D: 1
- C to E: 5
- C to F: 15
- D to E: 10
- D to F: 12
- E to F: 2
- G to A: 15
- G to B: 4
- G to C: 5
- G to D: 17
- G to E: 13
- G to F: 8
**Instructions:**
Use **Kruskal's Algorithm** to determine the minimum cost spanning tree for this graph. Then, draw the tree and provide its cost.
**Explaining Kruskal’s Algorithm:**
1. **Sort** all the edges in non-decreasing order of their weight.
2. **Initialize** the minimum spanning tree with no edges.
3. **Add edges** to the minimum spanning tree, one by one, using the sorted list, making sure no cycles are formed.
4. Stop when there are exactly \( V-1 \) edges in the tree, where \( V \) is the number of vertices in the graph.
**Purpose:**
This exercise will help in understanding how Kruskal’s algorithm can be applied for finding a minimum spanning tree in a graph, which is useful in network design, such as designing least cost networks.
Expert Solution
arrow_forward
Step 1
Please find the attachment
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- 2. For the below graph, find the minimum spanning tree. 8 2 4 9. 11 4 14 8 7. 8 6. 10 7 1 2arrow_forwardThe graph below shows the first four edges (in red) of a minimum spanning tree chosen with Kruskal's Algorithm. Find the weight of the next edge that will be added to the tree. 4 2 3 7 2 7, 8 5 5arrow_forward1) Using either Prim's or Kruskal's algorithms, determine the cost of the minimum spannin tree which will connect all the vertices of the graph below. State which algorithm you used. 5) Sketch the minimum spanning tree. 5 A F 4 J 2 2 2 4 B 8 G 1 K 13 3 7 C 5 H 4 L 2 2 1 D 7 I 3 1 12 2 E 6 Marrow_forward
- Consider the graph G below. 3. 6. 4 1 D 1 C 2 4 G 5 7 6. Use Kruskal's algorithm to calculate the length of the minimum spanning tree. Paragraph I Uarrow_forward40 is incorrectarrow_forward22 D 28 42 35. 45 20 B 44 E 29 A Find the minimum cost spanning tree on the graph above using Kruskal's algorithm. What is the total cost of the tree?arrow_forward
- 4. Find a minimum cost spanning tree on the graph below using Kruskal's algorithm. 20 7 13 14 17 21 9 3 18 12 19 8 16 15 11 22 1 10 2 Create a minimum spanning tree using Kruskal's algorithm. What is the total minimum length of the spanning tree?arrow_forwardThe graph below shows (in red) the first four edges of a minimum spanning tree chosen using Prim's Algorithm. Find the weight of the next edge that will be added to the tree. 2 8 2. 8 2 10 3 5 4 6, toarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

