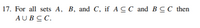
17. For all sets A, B, and C, if A C C and B CC then AUBCC.

Consider the following statement. Assume that all sets are subsets of a universal set U. For all sets A and B, if A C B then B C A°. Use an element argument to construct a proof for the statement by putting selected sentences from the following scrambled list in the correct order. Therefore, by definition of complement x E A, and thus, by definition of subset, B CA. Hence, x € A, because A NB = 0. By definition of complement, x € B. Suppose A and B are any sets such that AC B, and suppose x E B. If x were in A, then x would have to be in B by definition of subset. But x B, and so x A. Suppose A and B are any sets such that A C B, and suppose x E B. Proof: 1. .--Select--- 2.---Select--- 3. --Select--- 4. |--Select---

Let A1, · · · , An be countably infinite sets. Prove that A1 × A2 × · · · × An is countably infinite.