
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
22 plz answer all parts of the question
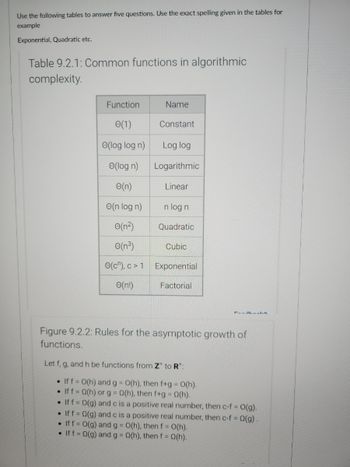
Transcribed Image Text:Use the following tables to answer five questions. Use the exact spelling given in the tables for
example
Exponential, Quadratic etc.
Table 9.2.1: Common functions in algorithmic
complexity.
Function
Name
(1)
(log log n)
e(log n)
e(n)
e(n log n)
e(n²)
0(³)
(c), c> 1 Exponential
e(n!)
Factorial
Constant
Log log
Logarithmic
Linear
n log n
Quadratic
Cubic
PULLLI-1.
Figure 9.2.2: Rules for the asymptotic growth of
functions.
Let f, g, and h be functions from Z to R¹:
• If f = 0(h) and g = O(h), then f+g = 0(h).
If f = Q(h) or g = Q(h), then f+g = Q(h).
• If f = O(g) and c is a positive real number, then c-f = 0(g).
• If f = Q(g) and c is a positive real number, then c-f = Q(g) .
• If f = O(g) and g = 0(h), then f = 0(h).
• If f = Q(g) and g = Q(h), then f = Q(h).
Transcribed Image Text:16
D
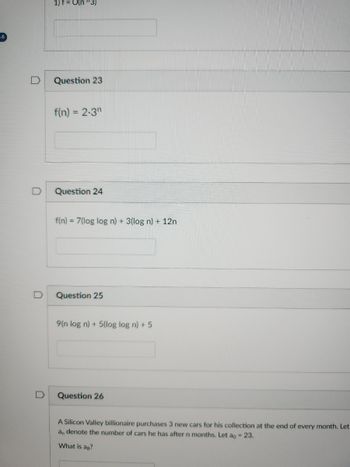
1) f = O(n^3)
Question 23
f(n) = 2.3
Question 24
f(n) = 7(log log n) + 3(log n) + 12n
Question 25
9(n log n) + 5(log log n) + 5
Question 26
A Silicon Valley billionaire purchases 3 new cars for his collection at the end of every month. Let
an denote the number of cars he has after n months. Let ao = 23.
What is ag?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 6 steps

Knowledge Booster
Similar questions
- Can you please provide your work. Thank youarrow_forwardMultiple Choice and Numerical Response *Record your answers on the front page* 1) How many 5 digit numbers can be made using the digits 5, 6, 1, 4, 9, 3, 2 if no digits can be repeated? A. 120 B. 2520 C. 21 D. 5040 2) Which of the following questions would result in a solution equal to 6P3? A A. Given the letters A, B, C, D, E, F, the number of 3 letter groups that can be made. B. Given 6 people in a club, the number of 6 person committees that are possible C. Given 6 people in a club, the number of ways that a president, secretary and treasurer can be assigned. D. Given 6 distinct cards, the number of 3 card hands that are possible. 3) How many arrangements can be made using all the letters in the word OSOYOOS.arrow_forwardIs 1.41 the answer to question A or B?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

