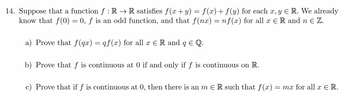
14. Suppose that a function f : R → R satisfies f(x+y) = f(x)+ f (y) for each x, y Є R. We already know that f(0) = 0, f is an odd function, and that f(nx) = nf(x) for all x = R and n ≥ Z. a) Prove that f(qx) = qf(x) for all x = R and q Є Q. b) Prove that f is continuous at 0 if and only if f is continuous on R. c) Prove that if f is continuous at 0, then there is an m Є R such that f(x) = mx for all x = R.

please explain and show all parts

The first Batman movie was made over 50 years ago in 1966. Över the years, Batman has been played on screen by a number of actors and even by a Lego figure in the Lego Batman movies. In the original comic books, Batman was 188 centimeters tall (about 6'2") and weighed 95 kilograms (about 210 pounds). The article "50 Years of Batman on Film: How Has His Physique Changed?"t included the heights and weights of all of the onscreen Batmen in the table below. Batman Height (cm) Weight (kg) Comic book 188 95 Lego Batman 4 0.005 Adam West 188 91 Michael Keaton 178 72 Val Kilmer 183 93 George Clooney 180 78 Christian Bale 183 82 Ben Affleck 193 98 A USE SALT With x = height and y = weight, the equation of the least squares regression line is ŷ = -3.0112 + 0.4881x. %D (a) Calculate the residuals. (Round your answers to two decimal places.)

Are they similar due to AA~