Question
thumb_up100%
Topic: Functions of a complex variable
Find the real and imaginary parts u(x, y) and v(x, y) of the following functions. Write it neatly and with complete details.
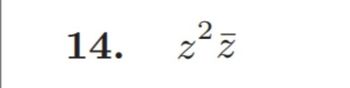
Transcribed Image Text:14.
2
וא
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- find u(x,y) , v(x,y) where f(z)=u+iv for function f(z)=Z2 e2zarrow_forwardGiven the points in space, A = (4,2,– 3), B = (-2,5,1), and C = (5,1,– 2) A) Find a parametric set of equations for the line through point A parallel to the line through points B and C. B) Find the equation of the plane containing points A, B, and C using a vector approach (from chapter 11). C) Find the coordinates of a point on the plane other than A, B, or C which does not lie on a coordinate axis. (no 0 coordinates)arrow_forwardUsing spherical polar coordinates r, 0, p to find CM of a uniform solid hemisphere of radius R, whose flat face lies in the xy plane with its center at the origin. The element of volume is in spherical polars of dV = r² dr sine de dip.arrow_forward
- Find the divergence and curl of each of the following vector functions: 1. S = < xy, 2yz, 3zx > 2. E = < y^2, (2xy+z^2), 2yz >arrow_forwardEvaluate the integral. dx (x – 4)(x – 3)(x + 5) | (Use symbolic notation and fractions where needed. Use C for the arbitrary constant.) dx %3D J (x – 4)(x – 3)(x + 5)arrow_forwardLet n 1 be an integer, let to to is given by a stationary path of the Lagrangian functional C: L[x] = 1 dt L(t,x,x), x(0) =x0, x(t)=X1, where LT - V and T is the total kinetic energy T = n 1 k=1 2 mark. Using the above first-integral, show that, if V is independent of t, the total energy E=T+V of the particle is a constant of the motion.arrow_forward
arrow_back_ios
arrow_forward_ios