11. Let n is a positive integer. Prove that n is even if and only if 3n²+1 is odd. (Hint: youmust prove bi-implication, it means p q = (p→q) ^ (q→ p).) 9. Let m, n are integers. Use a proof by contraposition to prove that if m*n is even, thenm is even or n is even.10. Let n be an integer. Use a proof by contradiction to prove that if 3n+2 is even, thenn is even.

Using a demonstration by contraposition, we will assume the negative of the conclusion and…

Answered: 11. Let n is a positive integer. Prove…

11. Let n is a positive integer. Prove that n is even if and only if 3n²+1 is odd. (Hint: you must prove bi-implication, it means p q = (p→q) ^ (q→ p).)

Database System Concepts

7th Edition

ISBN:9780078022159

Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Publisher:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Chapter1: Introduction

Section: Chapter Questions

Problem 1PE

See similar textbooks

Related questions

Q: Construct a truth table for (p--->(q--->r)) ---> ((p^q) V r)

A: A truth table is a mathematical tool used in logic to systematically evaluate the truth values of a…

Q: Prove or disprove each of the following

A: You have to be careful. The big-O is kind of like ≤≤, not like ==, but people forget that. For the…

Q: Suppose we have positive integers a, b, and c, such that that a and b are not relatively prime, but…

A: Suppose we have positive integers a, b, and c, such that that a and b are not relatively prime, but…

Q: Prove or disprove "Suppose that m and n are integers. If m > n ≥ 0, then gcd (m, n) = gcd (m − n,…

A: Prove or disprove "Suppose that m and n are integers. If m > n ≥ 0, then gcd (m, n) = gcd (m − n,…

Q: Solve the first-order linear recurrence T(n) = 3T(n-1) +8, T(0) = 6 by finding an explicit closed…

A: To solve the first-order linear recurrence relation: r(n) = 3T(n - 1) + 8, T(0) = 6 We can use the…

Q: 3. Using the pumping lemma and contradiction, prove that L = (a"b" n<m} is not regular.

A: We have to use the pumping lemma and contradiction theorem to prove the given statement: Statement:…

Q: 5. Let g(n) = log10 (n). Prove that g(n) = (lgn). Please show step by step solution. Show the work.

A: Given that, g(n)=log10(n) If we consider this as recurrence relation in the form aT(n/b)+nklogpn…

Q: Let f,g:Z+⟶R, and f(n)=nlog2(n) forn∈Z+. For which function g(n)below is f∉O(g)

A: The answer is given below step.

Q: Suppose f(n) = 19n³ and h(n) = 20n³ + n+ 23. Prove or disprove whether f(n) E N(h(n)) %3D Use the…

A: Here, we have to prove or disprove whether f(n) belongs to Ω(h(n)). As per the definition of Big…

Q: Consider functions f,g : N → R+ with g(n) > 2 for all n > 1. Is it true that f(n) O(g(n)) implies…

A: Given that, There are two functions f, g: N->R+ , g(n)>=2, n>=1 f(n)=O(g(n)) Big-Oh…

Q: L₁ = {anbman: n ≥ 0, m >0} Use the rule of contradiction, prove that following language is regular…

A: Given that:

Q: for n = 1 T(n) 2T(n/4) + /n log n for n > 1

Q: 5. Define the following (almost Fibonacci) recurrence for n = 0 Gn for n = 1 Gn-1+Gn-2+1 for n2 2…

A: Hey there, I am writing the required solution of the questin mentioned above. Please do find the…

Q: >>Y; is a matrix of polynomial coefficients of equation y= 3x³ + x² +6.

A: >>Y;---------- is a matrix of polynomial coefficients of equation y= 3x5+x²+6.[6,0,1,0,0,3]…

Q: 3. Given the following minterm expansion: F(a, b, c, d) = Em(0, 2, 3, 4, 8, 10, 11, 15) Draw the…

Q: Jason discovered that alarms can sing one of the n+1 tunes, which have the accompanying…

A: Here have to determine about the Song of the Sirens programming problem statement.

Q: Q Sum For parts (d) -(e), decide if it is true or false. If the statement is true, then prove it…

A: Introduction A mathematical language called asymptotic notation is used to represent how functions…

Q: 6. Suppose functions f(n) > 0 and g(n) > 0 satisfy f(n) = 0(9(n)). Prove or give a counterexample to…

A: Given that, f(n)>0, g(n)>0 and f(n)= O(g(n)) f(n)=n3, g(n)=n3+n, then f(n)= O(g(n)) is true.…

Q: Prove by induction that T(n) = 2T(n/2) + cn is O(n logn).

A: Induction is a mathematical proof technique where a statement is proven true for a base case, often…

Q: make an adjacency matrix for the following: E= {(1,2),(2,1),(3,2),(4,3),(4,5),(5,6),(6,7)}

A: In this question we have to construct a adjacency matrix program a given graph set Let's design a…

Q: If set A has size m, and set B has size n, then what is the size of the cross product of A and B?…

A: Introduction: A set is a collection of distinct and well-defined objects, which can be numbers,…

Q: Find GCD(25,150) by applying Euclid’s algorithm.

A: The solution for the above-given question is given below:

Q: Question : Prove L = {apbm : p,m\epsilonN} Note: Use Pumping lemma to solve this.

A: here we solve it: using pumping lemma check regular or not?:…

Q: Find upper bound of running time of quadratic function f(n) = 3n2 + 2n + 4. To find upper bound of…

Q: Let S be a circular arrangement of k integers with sum n. For 1 < j < n < 2k, prove that S has a…

A: Answer is given below-

Q: 3. Let g: Z→ Z be defined by g(m) = m + 5. Is Is g a bijection? Explain. If g is a bijection, find…

A: If a function has inverse it must be bijective. Bijective Function: If a function is said as the…

Q: 1. Big-O Notation Let fand g be functions from the set of integers or the set of real numbers to the…

A: Given that, f(x)= O(g(x)) that means f(x) is equal to big oh of g(x). Big-oh represents the tightest…

Q: Prove this matrix induction problem. Show every step to prove this.

A: To prove by induction that for positive integers n, n · G² 1]" = [F2n+1 F2n F2n-1], where G = [1 1;…

Q: Let B = {a + bi|a, b ∈ N}. Prove that B is countable.

A: Let B = {a + bi|a, b ∈ N}. Prove that B is countable. Theorem 2.3: handout on the cardinality and…

Q: (b) Prove: max(f(n), g(n)) E O(f(n)g(n)), i.e., s(n) E O(f(n)g(n)). Assume for all natural n, f(n) >…

A: Given that, f(n)>=1 and g(n)>=1 s(n)= max(f(n), g(n))

Q: 1. Using the Pumping Theorem, show that the language {a²´ | n > 0} is not regular.

A: Given, The answer is given below

Q: Question 2. (a) Show that there is no n EN such that n = 1 (mod 12) and n = 3 (mod 8). (b) Find a…

Q: Prove that {a"b"} is CFL but {a"b"c"} is not for n>=0.

A: Given , {a^nb^nc^n | n>=0}

Q: Prove that if x is odd, then x^2+ 3 is even.

A: Let x=3, Then x^2+ 3 = 3^ 2+3= 12 If x=5, Then x^2+ 3 = 5^2+3 =28 If x=7, Then x^2+ 3 = 7^2+3=52…

Q: 7. Let f(n)> g(n) denote that the first derivative of f(n) is larger than that of g(n). (25) Let…

Q: c) Prove that the following claim holds when for all n ≥1 Σ(8i-5)=4n²- n i=1 n

A: SOLUTION - In this problem, we need to prove : ∑i=1n(8i−5)=4n2−n PROOF - Taking left-hand side,…

Q: 4. Consider f(n) = 3n2 + 4n – 3, mathematically show that f(n) is O(n?), 2(n²), and O(n2).

Q: L = {w ∈ {a, b}∗ | the length of w is a multiple of 3 and w contains more a’s than b’s}. Use…

A: We need to demonstrate that there are infinitely many equivalence classes under the…

Q: Let f(n) = n2 and g(n) = 3n2 - 6n +4. Show that g(n) = 0(f(n)) by showing that there exist positive…

Question

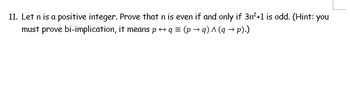
11. Let n is a positive integer. Prove that n is even if and only if 3n²+1 is odd. (Hint: you
must prove bi-implication, it means p q = (p→q) ^ (q→ p).)

9. Let m, n are integers. Use a proof by contraposition to prove that if m*n is even, then
m is even or n is even.
10. Let n be an integer. Use a proof by contradiction to prove that if 3n+2 is even, then
n is even.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1: Part(9)

VIEW

Step 2: Part(10)

VIEW

Solution

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 3 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.

Similar questions

We want to prove that f(n) = 1/n² +8√n + 1 is O(n²) using the formal definition introduced in class (i.e f(n) is O(g(n)) if there are two constant c and no such that f(n) ≤ c · g(n) for all n ≥ no). Which of the following pair(s) of constants c and no satisfy the definition? C = and no = C = 21 2 C = 19 and no 2 R 1/2 and no c = 10 and no = 1000 P = A. TA B 0 Consider the string s="BARBAPAPA". Which of the following trees is/are representing the optimal prefix codes obtained by the Huffman Algorithm? (Reminder: an edge to the left child encodes a 0, while an edge to the right child encodes a 1). 1 = = 4 A A 101010110110 10101001010110110 01100001100110011 R B 100001100011001100 B. TB P A) (R B P C. Tc A Using the codes from above, which of the following bit strings are valid encoding of s using Huffman Encoding? B R P D. Tp
Please answer it asap. both questions.
2
Prove that 2n = o(22n).
Suppose A is real n x n symmetric positive definite, and let A = LLT be its Cholesky decomposition. (a) Let n = 3 and write formulas for aij, i, j = 1,2,3, in terms of the entries of L. (b) Notice that if we consider the formulas in column order, we can compute the elements l11, 21, 31, l22, l32, and l33. Use this insight to write a MATLAB function to compute the Cholesky decomposition for a general value of n. Check the correctness of your function by comparing with chol.
Please solve using iterative method: Solve the following recurrences and compute the asymptotic upper bounds. Assume that T(n) is a constant for sufficiently small n. Make your bounds as tight as possible. a. T(n) = T(n − 2) + √n b.T(n) = 2T(n − 1) + c
Let f(n) and g(n) be asymptotically positive functions. Prove or disprove following. f(n) + g(n) = q(min(f(n), g(n))).
2) Prove divisible by 3 for any integer nzo. that n(n²+s) is divisible by 3 for Let n 1 1 (1² +5) = 1(1+5)=(6/ K(K²+5) K+ 1 ((k + 1 ) ² + 5
Prove that the sum of the first n odd positive integers is n2. In other words, show that 1 + 3 + 5 + .... + (2n + 1) = (n + 1)2 for all n ∈ N.
A. Show that if p(n) is a polynomial of the form n3 + C2 n? + c1 n + Co, then p(n) = O(n³).
4. Practice with the iteration method. We have already had a recurrence relation ofan algorithm, which is T(n) = 4T(n/2) + n log n. We know T(1) ≤ c.(a) Solve this recurrence relation, i.e., express it as T(n) = O(f(n)), by using the iteration method.Answer:(b) Prove, by using mathematical induction, that the iteration rule you have observed in 4(a) is correct and you have solved the recurrence relation correctly. [Hint: You can write out the general form of T(n) at the iteration step t, and prove that this form is correct for any iteration step t by using mathematical induction.Then by finding out the eventual number of t and substituting it into your generalform of T(n), you get the O(·) notation of T(n).]
Let f(n) y g(n) two positive asymptotic functions. Prove or disprove the following conjectures: a) f(n) = O(g(n)) implies 2f(n) = O(29(n)). b) f(n) = O(g(n)) implies g(n) = N(f(n)). c) g(n) = O((g(n))²).