Related questions
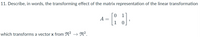
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps
I reached this same conclusion " Tx=Ax1x2⇒Tx=0110x1x2⇒Tx=x2x1" but had difficulty explaining it in words because it is only a reflection with respect to the y=x line if there is a negative value in either the x or y original vector.
eg. (-3,2) => (2,-3) reflects across the x and y axis
however if both values of x,y are negative of positive the values stay in the same quadrant and the reflection occurs over a corresponding diagonal midline.
As far as I can tell, the values are transpose
Sometimes online classes are extra difficult when asking for clarification isn't immediate or easy, so sorry for the needed follow up.
I reached this same conclusion " Tx=Ax1x2⇒Tx=0110x1x2⇒Tx=x2x1" but had difficulty explaining it in words because it is only a reflection with respect to the y=x line if there is a negative value in either the x or y original vector.
eg. (-3,2) => (2,-3) reflects across the x and y axis
however if both values of x,y are negative of positive the values stay in the same quadrant and the reflection occurs over a corresponding diagonal midline.
As far as I can tell, the values are transpose
Sometimes online classes are extra difficult when asking for clarification isn't immediate or easy, so sorry for the needed follow up.
- Find the standard matrix representation for each linear operator L : R^2 → R^2 described below:(a) L rotates each vector x by 45◦ in the clockwise direction. (b) L reflects each vector x about the x1 axis and then rotates it 90◦ in the counterclockwise direction. (c) L doubles the length of x and then rotates it 30◦ in the counterclockwise direction. (d) L reflects each vector x about the line x2 = x1 and projects it onto the x1 axis.arrow_forward3. Let T: R² R² be the linear transformation which first reflects points through the line X₁ = x₂ and then reflects points through the x₁-axis. a) Find the standard A matrix of T. b) Find all vectors v € R² such that v € Nul(A).arrow_forwardLet T: R² R² be the linear transformation which first reflects a vector through the x₁ -axis Chorizontal axis), and then rotates the resulting vector counterclockwise about the origin by I radions. [P+ 304 60. Find the standard matrix for T. to nous sotaov storb:00)arrow_forward
- Determine if the specified linear transformation is (a) one-to-one and (b) onto. Justify each answer. T(X1 X2 X3) = (x₁ - 4x2 +6x3, X2-9x3) (a) Is the linear transformation one-to-one? O A. T is one-to-one because the column vectors are not scalar multiples of each other. B. T is one-to-one because T(x) = 0 has only the trivial solution. O C. T is not one-to-one because the columns of the standard matrix A are linearly independent. O D. T is not one-to-one because the columns of the standard matrix A are linearly dependent.arrow_forwardThe cross product of two vectors in R³ is defined by Let = A = a₁ a2 a3 b1 [a2b3-a3b2] b2 = a3b1a1b3 ხვ La1b2-a2b1 H 1 Find the matrix A of the linear transformation from R³ to R³ given by T(z) = x *.arrow_forwardShow that T is a linear transformation by finding a matrix that implements the mapping. Note that x1, X2, ... are not vectors but are entries in vectors. T(x1 X2 X3) = (*1 -2x2 +5x3, X2 - 9x3) A= (Type an integer or decimal for each matrix element.)arrow_forward
- Show that T is a linear transformation by finding a matrix that implements the mapping. Note that x1, X2, ... are not vectors but are entries in vectors. T(X1,X2.X3) = (X1 - 8x2 + 7x3, X2 - 3x3) A = (Type an integer or decimal for each matrix element.)arrow_forwardWrite a detailed solution to the problem below and upload your answer to Gradescope. Define T : R² → R² by T(7) = T ([^]) = [ 3x1 2x2 2x2 • a) Let it = [ #] and 8 = [ ] ¹ be two vectors in R² and let c be any scalar. Prove that T is a linear transformation.arrow_forwardLet Tv = Av represent the linear transformation T: R2 → R3 where 1 2 A = -2 4 -2 2]arrow_forward
- 5. Consider a linear transformation T: R2 → R2 which reflects a vector about the line y=-x, and dilates the reflected vector by a factor of 2. Find the standard matrix for the linear transformation.arrow_forwardFind the matrix A of the linear transformation T from R2 to R² that rotates any vector through an angle of 150° in the clockwise direction. A =arrow_forwardSuppose that f : R² → R² is the linear transformation which first rotates a vector 90 degrees clock- wise and then multiplies the first coordinate by 2. Find a 2 × 2 matrix A such that f(x) = Ax for any vector x E R².arrow_forward
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
