Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
11. Solve, if necessary round to the nearest hundred
![The image displays a mathematical equation, which is problem number 11:
\[ 5 + \log_3(n + 1) = 8 \]
This equation involves solving for the variable \( n \) where a logarithmic expression with base 3 is used. Let's break it down step-by-step for better understanding:
1. **Understanding Logarithms**: The equation includes a logarithm base 3, written as \(\log_3(n + 1)\). This represents the power to which the base 3 must be raised to yield \( n + 1 \).
2. **Isolating the Logarithmic Term**: To solve for \( n \), first isolate the logarithmic term:
\[ \log_3(n + 1) = 8 - 5 \]
\[ \log_3(n + 1) = 3 \]
3. **Converting to Exponential Form**: Convert the logarithmic equation to its equivalent exponential form to solve for \( n + 1 \):
\[ n + 1 = 3^3 \]
4. **Solving the Exponential**: Calculate \( 3^3 \), which equals 27:
\[ n + 1 = 27 \]
5. **Finding \( n \)**: Subtract 1 from both sides to solve for \( n \):
\[ n = 27 - 1 \]
\[ n = 26 \]
Thus, the solution to the equation is \( n = 26 \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa93fe523-bbc5-4ded-98ad-9d42c9cf636e%2Ff58839b1-e184-4070-932b-664c357c6c2e%2F0mim2t_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The image displays a mathematical equation, which is problem number 11:
\[ 5 + \log_3(n + 1) = 8 \]
This equation involves solving for the variable \( n \) where a logarithmic expression with base 3 is used. Let's break it down step-by-step for better understanding:
1. **Understanding Logarithms**: The equation includes a logarithm base 3, written as \(\log_3(n + 1)\). This represents the power to which the base 3 must be raised to yield \( n + 1 \).
2. **Isolating the Logarithmic Term**: To solve for \( n \), first isolate the logarithmic term:
\[ \log_3(n + 1) = 8 - 5 \]
\[ \log_3(n + 1) = 3 \]
3. **Converting to Exponential Form**: Convert the logarithmic equation to its equivalent exponential form to solve for \( n + 1 \):
\[ n + 1 = 3^3 \]
4. **Solving the Exponential**: Calculate \( 3^3 \), which equals 27:
\[ n + 1 = 27 \]
5. **Finding \( n \)**: Subtract 1 from both sides to solve for \( n \):
\[ n = 27 - 1 \]
\[ n = 26 \]
Thus, the solution to the equation is \( n = 26 \).
Expert Solution
Step 1
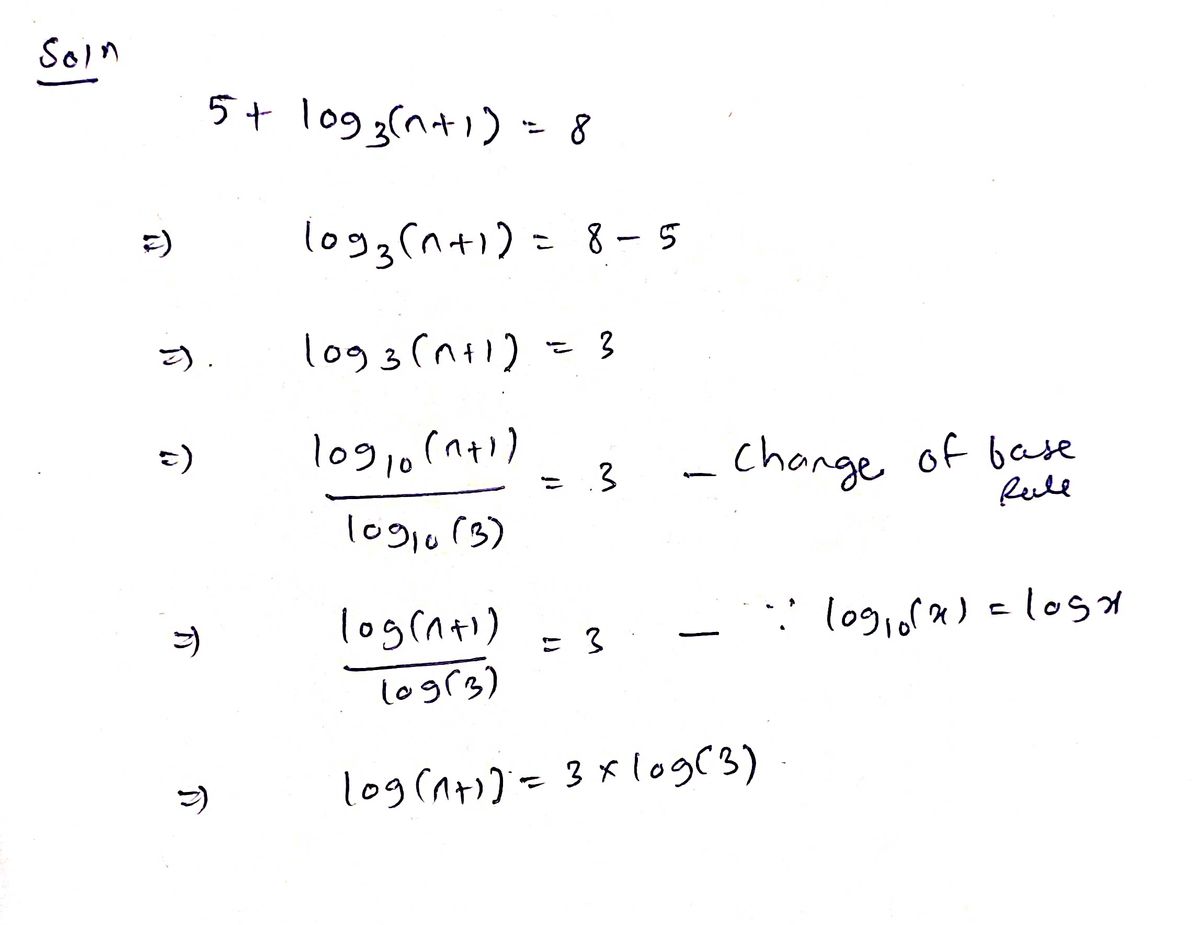
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education