A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
Scott wakes up late on average 3 days in every 5. If Scott wakes up late, the probability he’s late for school is 9/10. If Scott does not wake up late, the probability he’s late for school is 3/10. Complete the tree diagram to calculate what percent of the days Scott is late to school?
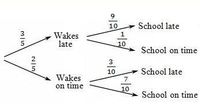
Transcribed Image Text:This image is a probability tree diagram used to determine the likelihood of arriving at school late or on time based on whether a person wakes up late or on time.
### Explanation of the Diagram:
1. **Initial Split**:
- The first decision point is whether the individual wakes late or on time.
- **Wakes late** has a probability of \( \frac{3}{5} \).
- **Wakes on time** has a probability of \( \frac{2}{5} \).
2. **Second Level Outcomes**:
- Given that a person wakes late:
- The probability of being **school late** is \( \frac{9}{10} \).
- The probability of being **school on time** is \( \frac{1}{10} \).
- Given that a person wakes on time:
- The probability of being **school late** is \( \frac{3}{10} \).
- The probability of being **school on time** is \( \frac{7}{10} \).
### Summary:
The tree structure helps visualize compound probabilities by breaking them into sequential stages. The probability of each outcome is computed by multiplying the probabilities along the branches. This tool is useful in educational settings for teaching probability concepts and decision-making processes.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- The amount of time spouses shop for anniversary cards can be modeled by an exponential distribution with the average amount of time equal to 58 minutes. What is the probability that a randomly selected spouse spends no more than 20 minutes shopping for an anniversary card?arrow_forwardThe average number of field mice per acre in a 5-acre wheat field is estimated to be 6. Find the probability that fewer than 4 field mice are found on 3 of the next 4 acres inspected.arrow_forwardA large bus company experience bus breakdowns at the rate of 2.5 per day. Find the probability that more than two breakdowns occur on two of the next 5 days.arrow_forward
- the probability of winning on an arcade game is0.568. if you play the arcade game 22 times, what is the probability of winning more that 15 times?arrow_forwardThe rate of failure in a year for a microSD card is 14%. if you have the same material backed up to 3 of them, what is the probability that at least one will be good?, find the probability that if you pick 3 memory cards, at least 1 will be good. Round to 3 decimalsarrow_forwardA machine has 32 identical components which function independently. The probability that a component will fail is 0.28. The machine will stop working if more than three components fail. Find the probability that the machine will be working. Round to the nearest thousandth.arrow_forward
- There is a 30% chance it will snow on any one of the next 5 days. What is the chance it will snow at least 2 of those days?arrow_forwardThe amount of time spouses shop for anniversary cards can be modeled by an exponential distribution with the average amount of time equal to 47 minutes. What is the probability that a randomly selected spouse spends at least 39 minute shopping for an anniversary card?arrow_forwardThe amount of time spouses shop for anniversary cards can be modeled by an exponential distribution with the average amount of time equal to 48 minutes. What is the probability that a randomly selected spouse spends more than 12 but less than 88 minutes shopping for an anniversary card?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON