Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Topic Video
Question
Find the values of x and y that minimize the objective function P=3x+2y for the graph. What is the maximum value
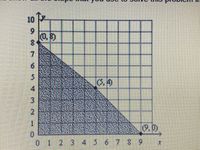
Transcribed Image Text:The provided image is a graph on a coordinate plane, showing a shaded triangular region. Below is a detailed description of its elements:
### Graph Description:
- The graph represents a section of the coordinate plane with axes labeled as \( x \) (horizontal axis) and \( y \) (vertical axis).
- The grid is divided into unit squares, with the x-axis and y-axis both ranging from 0 to 10.
### Points on the Graph:
- **Point (0, 8):** This point lies on the y-axis, at the intersection of \( x = 0 \) and \( y = 8 \).
- **Point (9, 0):** Located on the x-axis, at the intersection of \( x = 9 \) and \( y = 0 \).
- **Point (3, 4):** Positioned within the graph area inside the grid, at \( x = 3 \) and \( y = 4 \).
### Shaded Region:
- The shaded area forms a triangle bounded by the points (0, 8), (9, 0), and (0, 0).
- The hypotenuse of the triangle appears to be a line connecting (0, 8) to (9, 0), suggesting this is part of an inequality boundary or a defined linear region.
This graph can be used to visually represent systems of inequalities or explore concepts related to linear programming where feasible regions are determine under constraints represented by linear equations.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- A farmer wants to fence a rectangular pasture for his chickens with his 100m of fences. By graphing the equation fx) = -2x + 100x, he can determine what dimensions to use to maximize the fenced area. Which value on the graph will be the maximum length he can use? O a. x-intercept O b. y coordinate of maximum vertex Oc. y-intercept Od. x coordinate of maximum vertex Clear my choicearrow_forwardA class trip to a beach has been planned for your senior trip. The lifeguard is only on duty when the temperature is between 70 degrees and 105 degrees. There is room for 60 people on your trip. Write the constraints to represent this real-world problem, where x is the temperature and y is the number of people on your trip.arrow_forwardCompany A sells floor tiles which are 2 square feet in area, weigh 4 pounds, and cost $1. Company B sells floor tiles which are 3 square feet in area, weigh 2 pounds, and cost $2. Your job is to buy floor tiles to maximize the area covered, at a total cost of no more than $10 and a total weight of no more than 16 pounds. Please use the graph paper. Let X be the number of tiles from Company A, and Y be the number of tiles from Company B. Show your work. How many tiles do you buy from Company A? _______ How many tiles do you buy from Company B? _______arrow_forward
- A car rental agency rents 300 cars per day at a rate of $55 per day. For each $1 increase in the per-day rate, 3 fewer cars are rented. They want to know what price they should rent at to maximize their revenue. Help them get started by setting up the revenue equation. You do not need to find the optimal price, just set up the revenue equation. Use x as your variable, but in your work be sure to define what a represents. Revenue =arrow_forwardA cruise line sells tickets to two kinds of passengers, luxury and economy class. Suppose that economy passengers pay $ 400 per ticket, while luxury passengers pay $ 800. The cost (in hundreds of dollars) of taking a economy passengers and y luxury passengers is though to be x² 2xy 2y² + 400 200 100 C(x, y) = 3x + 5y + + +35 Your job is to find out how many tickets of each type would lead to the maximum profit. How many ecomony passengers would lead to the highest profit? How many luxury passengers would lead to the highest profit?arrow_forwardDraw the graph of y = 3x2 + 6x − 24 and label its minimum.arrow_forward
- One of the two tables below shows data that can best be modeled by a linear function, and the other shows data that can best be modeled by a quadratic function. Identify which table shows the linear data and which table shows the quadratic data, and find a formula for each model.arrow_forwardA business owner is monitoring the production cost of making laptop computers. It costs $5,000 to start the business. The production cost for 10 computers totals $6,000, and the production cost for 20 computers totals $5,000. Which type of function would best model the data, and why? Quadratic, because the production cost decreases to a minimum of $5,000 and then increases Quadratic, because the production cost increases to a maximum of $5,000 and then decreases Quadratic, because the production cost decreases to a minimum of $6,000 and then increases Quadratic, because the production cost increases to a maximum of $6,000 and then decreasesarrow_forwardBob wants to create two pens, as shown in the figure. One pen is for a garden and it needs a heavy duty fence to keep out the critters. This heavy duty fence costs $28 per foot. The dog pen shares a side with the garden and has a lighter weight fence on the other three sides that costs $7 per foot. If each pen is to have an area of 3,240, find the values of x and y that would minimize the total cost of the fencing. x= y=arrow_forward
- A sandwich store's weekly revenue is given by the function R(x) = -0.0001 x2 + 3 x. The graph of the revenue function has a minimum value of 15,000. True Falsearrow_forwardA paper manufacturing company converts wood pulp to writing paper and newsprint. The profit on a unit of writing paper is $500 and the profit on a unit of newsprint is $350. Solve, a. Let x represent the number of units of writing paper produced daily. Let y represent the number of units of newsprint produced daily. Write the objective function that models total daily profit. b. The manufacturer is bound by the following constraints: * Equipment in the factory allows for making at most 200 units of paper (writing paper and newsprint) in a day. * Regular customers require at least 10 units of writingpaper and at least 80 units of newsprint daily. Write a system of inequalities that models these constraints. c. Graph the inequalitiers in part (b) Use only the first quadrant, because x and y must both be positive. (Suggestion: Let each unit along the x- and y-axes represent 20.) d. Evaluate the objective function at each of the three vertices of the graphed region. e. Complete the missing…arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,