Question
1. Examine the charge distribution shown. Sphere 1 has a charge of +3.0 × 10-4C; sphere 2 has a charge of –3.0 × 10-4C; and sphere 3 has a charge of +3.0 × 10-4C. Assume that Coulomb’s constant, (k) is equal to 9.0×109 N × m2/c2
a) Determine the total electric potential energy for the charge distribution.
b) Determine the total electric potential at point Z.
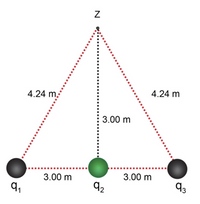
Transcribed Image Text:4.24 m
4.24 m.
3.00 m
3.00 m
3.00 m
q,
92
93
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps

Knowledge Booster
Similar questions
- a.) Calculate the speed of a proton that is accelerated from rest through an electric potential difference of 149 V. b.) Calculate the speed of an electron that is accelerated through the same potential difference.arrow_forward5. A uniform electric field of magnitude 250 V/m is directed in the positive x direction. A 112.0-µC charge moves from the origin to the point (x, y) = (20.0 cm, 50.0 cm). (a) What is the change in the potential energy of the charge-field system?arrow_forward4. charge moves a distance of 2.0 cm in the direction of a uniform electric field whose magnitude is 215 N/C. As the charge moves, its electrical potential energy decreases by 6.9 x10-19 J. Find the charge on the moving particle. What is the potential difference between the two locations?arrow_forward
- 2. A charge q = - 2.0 C moves in the opposite direction of a uniform electric field of 100 V/m by a distance of 3.0m. a. The charge is at a point of (a. higher, b. lower, c. same) potential before moving. b. After moving, the potential energy of the charge a. increases. b. decreases. c. does not change. c. What is the change in the potential energy?arrow_forward5. The Poisson equation 8² + ax² ay² az² relates the electrostatic potential (r) = (x, y, z) to the charge distribution p(r) in vacuum. In partic- ular, when we are dealing with a point charge, we write this equation as 7²4 = | 8² əx² + 8² 8² əz² 2² + o(r) + G 5, 8) = - = 10² G(r, r') p(r) €0 -83) (r-r'), where r' = (x, y, z) is the position of the point charge, 63) (r - r') = 6(x − x')8(y - y')6(z - z') is the Dirac delta function in three-dimensional space. Solve for G(r, r') by performing a three-dimensional Fourier transform on the Poisson equation, followed by a three-dimensional inverse Fourier transform. You may use the result 00 sin id=arrow_forward21. Two metal plates are charged and are measured to have a potential difference of 15.0 V. An electron is placed near the negative plate and released. What is the kinetic energy of the electron when it reaches the positive plate? a. 24.0 x 10¹ b. 9.9 x 10-¹9 1.0 x 10-¹9 J 13.4 x 10-19 j c. d.arrow_forward
- 1. Two point charges, +3 C and -6 C, are separated by 20 cm. They are NOT free to move. a) What is the magnitude of the electrostatic (Coulomb) force between the charges? Leave your answer as a function of k. ibuenser b) What is the electric field at the center point between the two charges? Leave your answer as a function of k. c) What is the electric potential at the center point between the two charges? Leave your answer as a function of k.arrow_forward5. You found that the electric potential due to a dipole oriented along the z axis is given by pco$e) 4те a. What is the direction of the field along the x axis? b. If we are on the x axis, a derivative with respect to z is the same as 1 d dz ф Use this equivalence to calculate Ez along the x axis. This should agree with your result from Unit VII p. 20 in your activity guidearrow_forwardA -15 nC charge and a 9 nC charge are located on the x-axis at x=-6 cm and x=9 cm respectively. iii.How far to the left of the -15nC charge does the electric potential equal -27V? iv.What is the magnitude (in N/C) of the electric field at this location?arrow_forward
arrow_back_ios
arrow_forward_ios