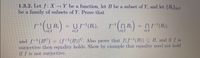
1.3.2. Let f: X → Y be a function, let B be a subset of Y, and let {B;}ie1 be a family of subsets of Y. Prove that U B, U(B.). B.) n (B.), iel iel iel iel and f-(BC) = (f-'(B))C. Also prove that f(-(B)) C B, and if f is surjective then equality holds. Show by example that equality need not hold if f is not surjective. %3D

plz solve question (c) with explanation within 30-40 mins and get upvotes

Used cars 2010 Vehix.com offered several used ToyotaCorollas for sale. The following table displays the ages ofthe cars and the advertised prices. a) Make a scatterplot for these data.b) Do you think a linear model is appropriate? Explain.c) Find the equation of the regression line. d) Check the residuals to see if the conditions for infer-ence are met. Age (yr) Price ($) Age (yr) Price ($)1 15988 6 99951 13988 6 119882 14488 7 89903 10995 8 94883 13998 8 89954 13622 9 59904 12810 10 41005 9988 12 2995

What is the variable requirement for a chi-square analysis?