
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
![1.3.2 Determine which of the following functions are and
are not linear forms.
*(a) The function f : R" → R defined by f(v) = ||v||.
(b) The function f: F"F defined by f(v) =v1.
%3D
*(c) The function f: M2 M2 defined by
chip
f
b.
a]
%3D
d
[d
b.
C
(d) The determinant of a matrix (i.e., the function det:
Mn →F).
*(e) The function g : P → R defined by g(f)= f'(3),
where f' is the derivative of f.
(f) The functiong:C → R defined by g(f) = cos(f(0)).](https://content.bartleby.com/qna-images/question/5d456ce1-cbfb-470f-8ef9-05bd7d57f044/a714b69a-af94-4678-aece-679e4c42d492/prmu3uo_thumbnail.jpeg)
Transcribed Image Text:1.3.2 Determine which of the following functions are and
are not linear forms.
*(a) The function f : R" → R defined by f(v) = ||v||.
(b) The function f: F"F defined by f(v) =v1.
%3D
*(c) The function f: M2 M2 defined by
chip
f
b.
a]
%3D
d
[d
b.
C
(d) The determinant of a matrix (i.e., the function det:
Mn →F).
*(e) The function g : P → R defined by g(f)= f'(3),
where f' is the derivative of f.
(f) The functiong:C → R defined by g(f) = cos(f(0)).
Expert Solution
arrow_forward
Step 1
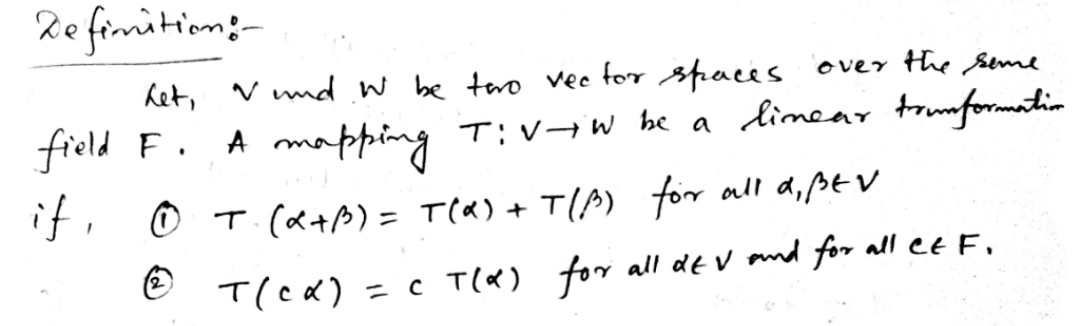
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- T: V ---> V is a linear operator with a B and B' ordered bases for V a. Find the matrix representation for T relative to the ordered bases B and B' b. Find T(v), using a direct computation and using the matrix representationarrow_forward[4 2 4] 0 6 [4 6 4] Q1\ Assume A = 1- Find value of x that made A symmetric matrix 2- Find cofactor for x 3- Find determinant of .arrow_forwarda. compute determinant of matrix A b. check invertibility c. compute determinant of B when B = A^3arrow_forward
- 4. Let E: P3 R2 be given by E (p(x)) = [P(2)] (a) Find a matrix that induces the transformation E. TH (b) Find a polynomial p(z) where E(p(x)) = [], or explain why this isn't possible. (c) Find a polynomial q(2) where E(q(z)) = [], or explain why this isn't possible. 8P (d) Find a nonzero polynomial r(z) where E(r(2)) = [] or explain why this isn't possible. (e) Describe the kernel of E. What is the dimension of the kernel? Find a basis for the kernel. (f) Describe the image of E. What is the dimension of the image? Find a basis for the image. (g) Is the transformation E one to one? Is it onto? Is it an isomorphism? Explain.arrow_forward(){88 B} (e) None of the above Problem 4. Let u = = and v are both solutions to Ax (a) det A = -1 (b) det A = 0 (c) det A = 1 (d) det A = 9 (e) None of the above 2 and b = 1 Let A be a 3 x 3 matrix such that u What is the determinant of A?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

