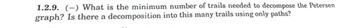
1.2.9. (-) What is the minimum number of trails needed to decompose the Petersen graph? Is there a decomposition into this many trails using only paths?

Kn,n,n be a complete 3-bipartite graph whose maximal independent sets are C1 = [n],C2 = [2n] – [n], and C3 = [3n] – [2n]. - (a) How many edges does Kn,n,n have? (b) Does Kn,n,n have an Eulerian cycle? (c) Show by any means that Kn,n,n has a Hamilton cycle. (d) Let G be the graph that is obtained from Kn,n,n by removing the edges of your Hamilton cycle. Does G have an Eulerian cycle?

1. Fifteen balls, including three each of five different colors, are arrange in a triangle as shown. How many ways can this be done if arrangements obtained by rotations are considered the same? 2. (a) Construct the cycle index polynomial for coloring the faces of the regular tetrahedron. (There are 12 rotations including the identity that map the regular tetrahedron, as a rigid body in 3-space, into itself.) (b) Find the number of ways to paint the faces of a tetrahedron using k colors, for each k = 2, 3, 4. 3. (a) Compute the cycle index polynomial for the group of rotations of the cube represented as permu- tations of the six faces. (There are 24 rotations including the identity that map the cube, as a rigid body in 3-space, into itself. We are ignoring the 24 reflections of the cube.) What is the number of essentially different ways to paint the faces of the cube in 2 colors? In 3 colors? In n colors? (b) What is the number of essentially different ways to paint the faces of a cube…

Show that Z3 X Z5 is cyclic.

Construct a Cayley table for U(12)

2. A k-dimensional hypercube on 2^k vertices is defined recursively. The base case, a 1-dimensional hypercube, is the line segment graph. Each higher dimensional hypercube is constructed by taking two copies of the previous hypercube and using edges to connect the corresponding vertices (these edges are shown in gray). Here are the first three hypercubes: 1D: 2D: 3D: • Draw the four-dimensional hypercube. • Find a recursive formula for the number of edges in a k-dimensional hypercube in terms of the number of edges and the number of vertices in a k-1 dimensional hypercube. • Find the closed form of the recursive formula in part b.

2