
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
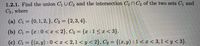
Transcribed Image Text:### Section 1.2.1: Set Operations
**Objective:** Find the union \( C_1 \cup C_2 \) and the intersection \( C_1 \cap C_2 \) of the two sets \( C_1 \) and \( C_2 \), where:
#### (a) Discrete Sets
- \( C_1 = \{0, 1, 2\} \)
- \( C_2 = \{2, 3, 4\} \)
#### (b) Continuous Sets on the Number Line
- \( C_1 = \{x : 0 < x < 2\} \)
- \( C_2 = \{x : 1 \leq x < 3\} \)
#### (c) Sets in the Cartesian Plane
- \( C_1 = \{(x, y) : 0 < x < 2, 1 < y < 2\} \)
- \( C_2 = \{(x, y) : 1 < x < 3, 1 < y < 3\} \)
**Explanation of Operations:**
- **Union (\( C_1 \cup C_2 \))**: Combines all elements from both sets without repetition.
- **Intersection (\( C_1 \cap C_2 \))**: Includes only elements that are present in both sets.
**Graphical Representation**:
- For continuous sets (b), visualize on a number line.
- For Cartesian plane sets (c), consider rectangles or regions on a plane.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- 8. If the graph of h(x) goes through the points A(-16,4), B(-4,0), C(0,-4) and D(4,16), then how many of the following statements are true for the graph of h(x) ? Point A will be mapped onto A'(-16,2). II. Point B will be an invariant point. III. Point C will be an invariant point. IV. Point D will be mapped onto D' (2,16) I. А. one B. two C. three D. four ZEBRA Mild Ink M IL DLI NER. -V5 А. V5 В. 5 2/5 С. - 2/5 D. Tiw doidw 10. If cos0 = V3 sin O then the exact value of tan 20 is: A. -V3 В. 2/3 D. 3 С.arrow_forwardGiven f(x)= a) (f+g)(x) c) (f- g)(x) 5x x-4 e) (f.g)(x) and g(x)= b) the domain of (f + g)(x) in interval notation g) 2) (1) (²) 6 x + 2 h) the domain of find the following. 5x2 + 16x-24 x²2x 8 d) the domain of (f - g)(x) in interval notation (1) ( (-∞,-2) U (-2,4) U (4,00)✓ 5x² + 4x + 24 x² 2x 8 f) the domain of (f g)(x) in interval notation (−,−2) U(−2,4) U (1,0) v ở 30x (x-4)(x+2) ✓ (-∞0,-2) U (-2,4) U (4,00)✓ () in interval notationarrow_forward▼x (-y +x, x² + 3zy, zxy³) =? O (3y-3zx², zx³, -2 + x) O(-3y-3x²z, yz, 1+ 2z) O(-3y + 3xy²z, -y³z, 1+ 2x) O (2y + x² z, yz³, 1+ 2x) ○ (−3y + 3x² yz, −y³z, 1 + x)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

