
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
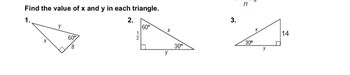
Transcribed Image Text:**Instructions: Find the value of x and y in each triangle.**
1. **Triangle 1**
- Given: A right triangle with angles 60° and a right angle.
- Sides: One side marked as 8 (adjacent to the right angle) and the other sides labeled as x and y.
2. **Triangle 2**
- Given: A right triangle with angles 60°, 30°, and a right angle.
- Sides: The shorter leg opposite the 30° angle is marked as 1/2. The hypotenuse is labeled as x, and the other leg (adjacent to the 30° angle) is labeled as y.
3. **Triangle 3**
- Given: A right triangle with angles 30° and a right angle.
- Sides: The hypotenuse is marked as 14, with the other sides labeled x (opposite the 30° angle) and y.
**Explanation for Solving:**
To find the values of x and y in these right triangles, one can use trigonometric ratios or specific properties of 30°-60°-90° triangles:
- In a 30°-60°-90° triangle, the ratio of side lengths is 1 : √3 : 2. For example, the side opposite the 30° angle is half the hypotenuse, and the side opposite the 60° angle is the shorter leg times √3.
- Use these properties, along with the Pythagorean theorem if needed, to find the unknown sides.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning