
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
1. Using the functions for each student, predict how many shares each student's post will be received on Day 3 and then on Day 10. Justify your answers.
2. If Amber decides to mail copies of her photo to the 45 residents of her grandmother's assisted living facility, the new function representing her photo shares is f(x) = 3(4)x + 45. How does this graph compare with the original graph of Amber's photo share?
3. Based on your results, which students' post travels the fastest? How is this shown in the equation form of the functions?
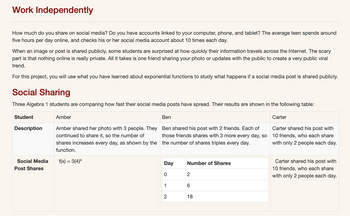
Transcribed Image Text:Work Independently
How much do you share on social media? Do you have accounts linked to your computer, phone, and tablet? The average teen spends around
five hours per day online, and checks his or her social media account about 10 times each day.
When an image or post is shared publicly, some students are surprised at how quickly their information travels across the Internet. The scary
part is that nothing online is really private. All it takes is one friend sharing your photo or updates with the public to create a very public viral
trend.
For this project, you will use what you have learned about exponential functions to study what happens if a social media post is shared publicly.
Social Sharing
Three Algebra 1 students are comparing how fast their social media posts have spread. Their results are shown in the following table:
Student
Description
Social Media
Post Shares
Amber
Ben
Amber shared her photo with 3 people. They Ben shared his post with 2 friends. Each of
continued to share it, so the number of those friends shares with 3 more every day, so
shares increases every day, as shown by the the number of shares triples every day.
function.
f(x) = 3(4)x
Day
0
1
2
Number of Shares
2
6
18
Carter
Carter shared his post with
10 friends, who each share
with only 2 people each day.
Carter shared his post with
10 friends, who each share
with only 2 people each day.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 10 images

Knowledge Booster
Similar questions
- Write an equation for the function graphed below 4. 12 1. - 7 -6-5 -4 -3 -2 1 2 4 6. -2 31 y =arrow_forwardStudent Loans Data for selected years from 2011and projected to 2023 can be used to show that thebalance of federal direct student loans y, in billions ofdollars, is related to the number of years after 2010,x, by the function y = 130.7x + 699.7.a. Graph the function for x-values corresponding2010 to 2025.b. Find the value of y when x is 13.c. What does this function predict the balance offederal direct student loans will be in 2029?(Source: U.S. Office of Management and Budget)arrow_forwardWrite an equation for the function graphed below 5+ 4 3- 2 1+ -7 -6 -5 -4 -3 -2 -1 -1 1 23 4 6 7 -2 -3+ -4- -5+ y%3D 5.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

