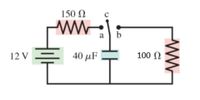
1. The capacitor in the figure is initially uncharged and the switch is at position c and not connected to either side of the circuit. At t = 0, the switch is flipped to position a for 20 ms,thenflipped back to position c for 10 ms, then flipped to position b for 20 ms, and finally flipped toposition c again. a) Using the Kirchhoff Voltage Law, write the differential equationsthat describethe circuit between t = 0 –20 ms andt = 30 –50 ms. b) Solve two differential equations you find ina) with appropriate initial condition to find the current through and the voltage across the capacitor as functions of time.
#1. The capacitor in the figure is initially uncharged and the switch is at position c and not connected to either side of the circuit. At t = 0, the switch is flipped to position a for 20 ms,thenflipped back to position c for 10 ms, then flipped to position b for 20 ms, and finally flipped toposition c again.
a) Using the Kirchhoff Voltage Law, write the differential equationsthat describethe circuit between t = 0 –20 ms andt = 30 –50 ms.
b) Solve two differential equations you find ina) with appropriate initial condition to find the current through and the voltage across the capacitor as functions of time.
c) Sketch the graphs of the current and voltage you find in b) from t = 0 to 60 ms.
#2. Now the 40 uF capacitor in the circuit in #1 is replaced with a 0.4 H inductor. The inductor in this circuit is initially uncharged and the switch is at position c and not connected to either side of the circuit. At t = 0, the switch is flipped to position a for 20 ms, then flipped back to position c for 10 ms, then flipped to position b for 20 ms, and finally flipped to position c again.
a) Draw a diagram for this circuit.
b) Using the Kirchhoff Voltage Law, write the differential equations that describe the circuit between t = 0 – 20 ms and t = 30 – 50 ms.
c) Solve two differential equations you find in b) with appropriate initial condition to find the current through and the voltage across the capacitor as functions of time.
d) Sketch the graphs of the current and voltage you find in c) from t = 0 to 60 ms.
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 1 images
