
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Please answer number 1, 2 and 3 for me thanks in advance. please show all steps and be clear thanks

Transcribed Image Text:The following picture represents a network of interconnected pipelines. The arrows represent the flow
measured by ft³ per minutes. The values above the arrows represent the flow in the given segment,
the flow is regulated by the valves at the intersections.
Of course the amount of water per minute entering each connection, has to be equal to the amount of
water exiting the connection. This leads to five equations.
10
20
40
6
Write down the system of linear equations that represents the flow at each relevant valve.
7
Find the augmented matrix and its row reduced echelon form.
8
How many solutions are there? Notice that the valves allow only one direction for the flow.
This means that we require each r; not to be negative. A solution with all positive r; is called
feasible.
9
Express all the feasible solutions in terms of inequalities.
Suppose you will need to repair the pipe between connections A and B, you will want to have
10 the flow between A and B as minimal as possible. What is the minimal value of æg to have a
feasible solution.
11 Using what you found in the previous answer write all the values of ri, for i = 1, ..., 6 and make
sure they are a solution of your system.
What happens if you reverse the flow in the segment BD (by substituting the valve)? Find the
12 minimal value of r6 that gives you a feasible solution.
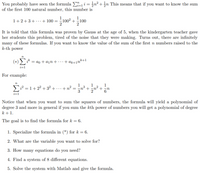
Transcribed Image Text:You probably have seen the formula E- i = }n² + }n This means that if you want to know the sum
of the first 100 natural number, this number is
1
+-100
1+2+3+ ...+ 100 =
It is told that this formula was proven by Gauss at the age of 5, when the kindergarten teacher gave
her students this problem, tired of the noise that they were making. Turns out, there are infinitely
many of these formulas. If you want to know the value of the sum of the first n numbers raised to the
k-th power
¿* = ao + a¡n + . .+ ak+1nk+1
ik
For example:
1
1
E² = 1+22 + 32 + · . + n² =
+교 + 공
i=1
Notice that when you want to sum the squares of numbers, the formula will yield a polynomial of
degree 3 and more in general if you sum the kth power of numbers you will get a polynomial of degree
k+1.
The goal is to find the formula for k = 6.
1. Specialize the formula in (*) for k = 6.
2. What are the variable you want to solve for?
3. How many equations do you need?
4. Find a system of 8 different equations.
5. Solve the system with Matlab and give the formula.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Find the distance between (-1.509, 1.15) and (-1.891, 0.996). What is the time traveled if 1 unit= 0.66 mile?arrow_forwardPlease be specificarrow_forwardPlease write the steps of this question and circle the answer so that I can understand. Please write the answer in an organized way if possible so that I can understand and identify the numbers. For each step, please specify which answer corresponds to which step. I appreciate your understanding. This question has several steps and I have sent you both pages. Please, if possible, write the step by step and circle the answer so that I don't get lost. Please tell me what the answer to each question is about.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

