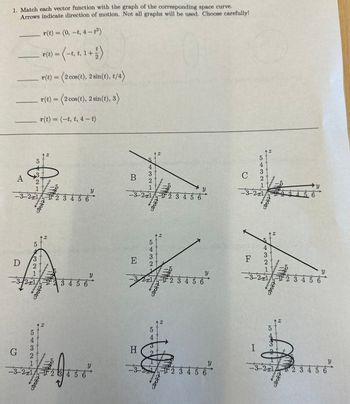
1. Match each vector function with the graph of the corresponding space curve. Arrows indicate direction of motion. Not all graphs will be used. Choose carefully! r(t) = (0, -t, 4-t²) r(t) = (-t, t, 1 + 1 ) r(t) = (2 cos(t), 2 sin(t), t/4) r(t) = (2 cos(t), 2 sin(t), 3) r(t) = (-t, t, 4-t)

Suppose that a bee is approaching a flower following the trajectory x = t° – 3t, y = t². Please note: Parts (a) and (b) should be written on one page, parts (c) and (d) - on the next page. (a) Find equation(s) of the tangent line(s) at (0, 3); (b) Find the coordinates of the points where the bee is flying horizontally and vertically; (c) Where is the trajectoty concave up and down? (d) Draw a rough sketch of the trajectory, indicating your findings about tangent lines. Hint: Use values of t = +2, ±V3, ±1,0.

How would I answer the directional derivative question attached in the image? Any help would be greatly appreciated :)