Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
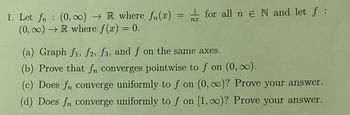
Transcribed Image Text:1. Let fn (0, ∞) → R where fn(x)
(0, ∞) → R where f(x) = 0.
=
nx
for all ne N and let f
(a) Graph f1, f2, f3, and f on the same axes.
(b) Prove that fn converges pointwise to f on (0, ∞).
(c) Does fn converge uniformly to f on (0, ∞o)? Prove your answer.
(d) Does fn converge uniformly to f on [1, ∞)? Prove your answer.
![(0,0)
Ex.
Let S = [0, 1] x fn(x) = x^ *nexo & 0≤x²1
or 5 to f(x) = { 1 + x = 1
Jaim: {fr} Conv. ptwise
(₁,1)
f(x)=x² = x to ¼/a ft = (1/2)
fa (x) = x²
fa= 1/4
f3 (x)=x²
9 f¶ (x) = .
=X
lim
So txES, 200
limm
Eanx"
lim
Bf Suppose 0≤x²1 - Then apo fn(x) = (im X"=0
Cim
lim
1^ ==
Suppose X=1. Then
2-01-1
4
sao fn(x) =
fn (x) exists,
S₁ = 90 x°
S₂ = 96x° +9₁x = 90 +9₁ x
S3 = ax +9₁ x + 9₂x²
= 90
+3 = ½
Does {fr} Conv. pluise on s? nf
Show of = 1
0
Sofn (x) dx = Area of A = 1/2 ² 1/0 +0=1
but So f(x) dx=0 lim
S = [0, 1] for 122, define fn (x) = ['n³x if 0≤x≤/n
2-n²(x - ²) 2 % ≤ x ≤
-0 i 3/ / LX ≤I
fn
15-01-
din f
Lim So fm (x) dx # Sr f(x) dx](https://content.bartleby.com/qna-images/question/79599c56-a340-49a0-b0ff-829b3947a798/b1850726-c7e3-4a6d-ad7d-33981e06e13b/xd10o4_processed.jpeg)
Transcribed Image Text:(0,0)
Ex.
Let S = [0, 1] x fn(x) = x^ *nexo & 0≤x²1
or 5 to f(x) = { 1 + x = 1
Jaim: {fr} Conv. ptwise
(₁,1)
f(x)=x² = x to ¼/a ft = (1/2)
fa (x) = x²
fa= 1/4
f3 (x)=x²
9 f¶ (x) = .
=X
lim
So txES, 200
limm
Eanx"
lim
Bf Suppose 0≤x²1 - Then apo fn(x) = (im X"=0
Cim
lim
1^ ==
Suppose X=1. Then
2-01-1
4
sao fn(x) =
fn (x) exists,
S₁ = 90 x°
S₂ = 96x° +9₁x = 90 +9₁ x
S3 = ax +9₁ x + 9₂x²
= 90
+3 = ½
Does {fr} Conv. pluise on s? nf
Show of = 1
0
Sofn (x) dx = Area of A = 1/2 ² 1/0 +0=1
but So f(x) dx=0 lim
S = [0, 1] for 122, define fn (x) = ['n³x if 0≤x≤/n
2-n²(x - ²) 2 % ≤ x ≤
-0 i 3/ / LX ≤I
fn
15-01-
din f
Lim So fm (x) dx # Sr f(x) dx
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- What is x divided by 0?arrow_forwardLook at the measurements for the rectangles that are scaled copies of the full sheet of paper. What do you notice about the measurements of these rectangles? Look at the measurements for the rectangles that are not scaled copies of the full sheet. What do you notice about these measurements?arrow_forwardCan someone explain x-bar to me?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,