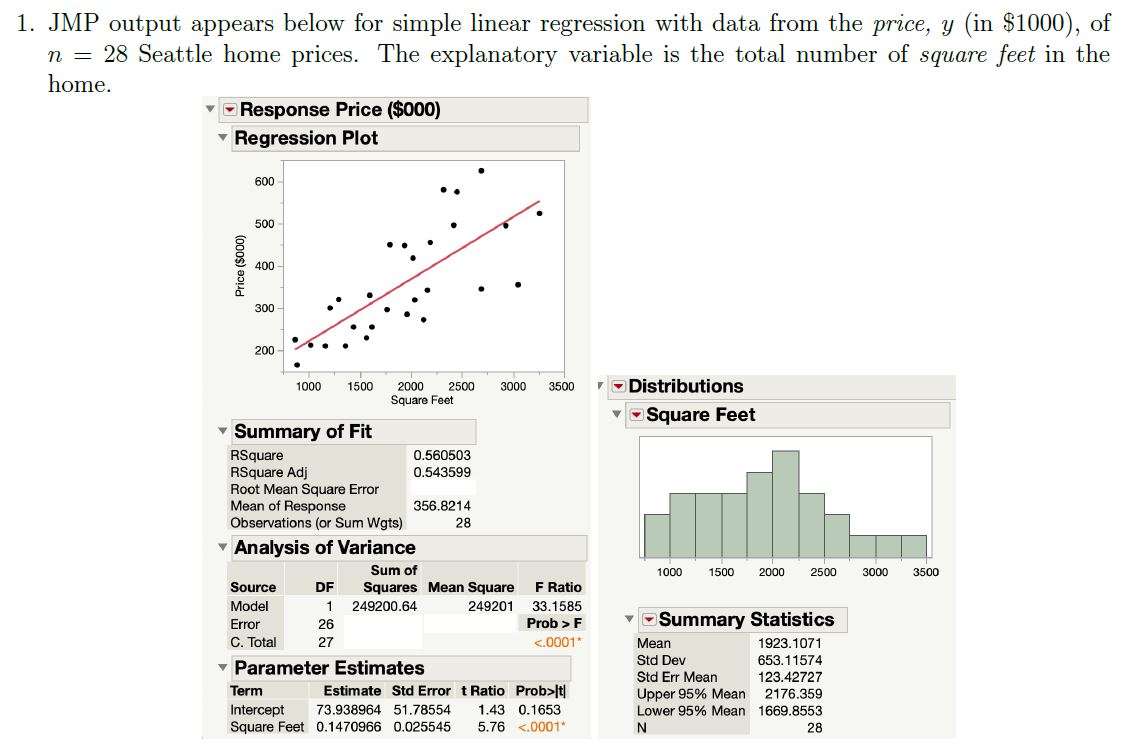
1. JMP output appears below for simple linear regression with data from the price, y (in $1000), of n = 28 Seattle home prices. The explanatory variable is the total number of square feet in the home. VOResponse Price ($000) v Regression Plot 600 500 400 300 200 1000 1500 2000 2500 3000 3500 DDistributions Square Feet Square Feet Summary of Fit RSquare RSquare Adj Root Mean Square Error Mean of Response Observations (or Sum Wgts) 0.560503 0.543599 356.8214 28 v Analysis of Variance Sum of 1000 1500 2000 2500 3000 3500 Source DF Squares Mean Square F Ratio Model 249200,64 249201 33.1585 Prob > F Summary Statistics Error 26 C. 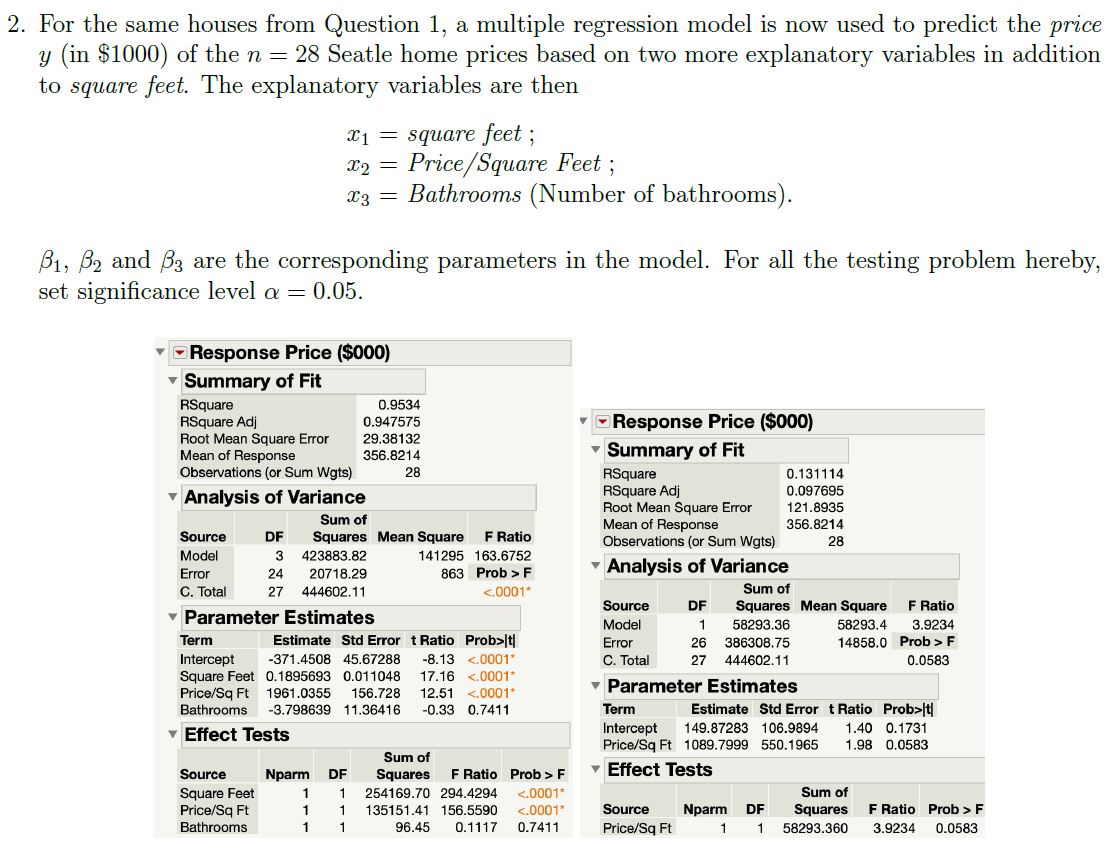Total 27 <.0001* Mean 1923.1071 653,11574 123.42727 Std Dev - Parameter Estimates Std Err Mean Term Estimate Std Error t Ratio Prob>lt| Upper 95% Mean Lower 95% Mean 1669.8553 2176.359 1.43 0.1653 Intercept Square Feet 0.1470966 0.025545 73.938964 51.78554 5.76 <.0001" 28 Price ($000) 2. For the same houses from Question 1, a multiple regression model is now used to predict the price y (in $1000) of the n = 28 Seatle home prices based on two more explanatory variables in addition to square feet. The explanatory variables are then X1 = square feet ; Price/Square Feet; Bathrooms (Number of bathrooms). B1, B2 and B3 are the corresponding parameters in the model. For all the testing problem hereby, set significance level a = 0.05. Response Price ($000) Summary of Fit RSquare RSquare Adj Root Mean Square Error Mean of Response Observations (or Sum Wgts) 0.9534 0.947575 29.38132 Response Price ($000) Summary of Fit 356.8214 28 RSquare RSquare Adj Root Mean Square Error Mean of Response Observations (or Sum Wgts) 0.131114 0.097695 v Analysis of Variance 121.8935 Sum of 356.8214 Source DF Squares Mean Square F Ratio 28 Model 423883.82 141295 163.6752 Analysis of Variance Error 24 20718.29 863 Prob > F C. Total 27 444602.11 <.0001* Sum of Source DF Squares Mean Square F Ratio v Parameter Estimates Model 58293.36 58293.4 3.9234 Term Estimate Std Error t Ratio Prob>|t| 14858.0 Prob > F 0.0583 Error 26 386308.75 C. Total Intercept Square Feet 0.1895693 0.011048 Price/Sq Ft -371.4508 45.67288 -8.13 <.0001* 27 444602.11 17.16 <.0001* v Parameter Estimates 12.51 <.0001* -0.33 0.7411 1961.0355 156.728 Bathrooms -3.798639 11.36416 Term Estimate Std Error t Ratio Prob>|t| Intercept Price/Sq Ft 1089.7999 550.1965 v Effect Tests 149.87283 106.9894 1.40 0.1731 1.98 0.0583 Sum of Nparm F Ratio Prob > F Effect Tests Source DF Squares Square Feet Price/Sq Ft Bathrooms 254169.70 294.4294 <.0001* Sum of 135151.41 156.5590 <.0001* Source Nparm DF Squares F Ratio Prob > F 1 96.45 0.1117 0.7411 Price/Sq Ft 58293.360 3.9234 0.0583

High School Graduates The following table shows the number, in millions, graduating from high school in the United States in the given year. Year Number graduating in millions 1985 2.83 1987 2.65 1989 2.47 1991 2.29 a. By calculating difference, show that these data can be modeled using a linear function. b. What is the slope for the linear function modeling high school graduations? Explain in practical terms the meaning of the slope. c. Find a formula for a linear function that models these data. d. Express, using functional notation, the number graduating from high school in 1994, and then use your formula from part c to calculate that value.

Life Expectancy The following table shows the average life expectancy, in years, of a child born in the given year42 Life expectancy 2005 77.6 2007 78.1 2009 78.5 2011 78.7 2013 78.8 a. Find the equation of the regression line, and explain the meaning of its slope. b. Plot the data points and the regression line. c. Explain in practical terms the meaning of the slope of the regression line. d. Based on the trend of the regression line, what do you predict as the life expectancy of a child born in 2019? e. Based on the trend of the regression line, what do you predict as the life expectancy of a child born in 1580?2300

Can the average rate of change of a function be constant?

Nikul

Type the regression equation for “Area” and “Biomass” in context into your document.   Interpret the slope of the regression line (in context of this data set) for “Area” and “Biomass”. is it meaningful to interpret the y-intercept for “Area” and “Biomass”? Why or why not?

A microcomputer manufacturer has developed a regression model relating his sales (y=$10,000s) with three independent variables. The three independent variables are price per unit(Price in $100s), advertising( ADV in $1000s) and the number of product lines (Lines). Part of the regression results is shown below.                            Coefficient                  Standard Error Intercept          1.0211                           22.8752 Price(X1)           -0.1524                          0.1411 ADV (X2)            0.8849                          0.2886 Lines(X3)           -0.1463                          1.5340     Source              d.f.                                 S.S. Regression       3                                     2708.61 Error                 14                                   2840.51 Total                 17                                   5549.12   What has been the sample size (n) for this analysis? Use the above results to find the estimated multiple…

please assist

Louis Katz, a cost accountant at Papalote Plastics, Inc. (PPI), is analyzing the manufacturing costs of a molded plastic telephone handset produced by PPI. Louis's independent variable is production lot size (in 1,000's of units), and his dependent variable is the total cost of the lot (in $100's). Regression analysis of the data yielded the following tables.     Coefficients Standard Error t Statistic p-value Intercept 3.996 1.161268 3.441065 0.004885 x 0.358 0.102397 3.496205 0.004413   Source df SS MS F   Se = 0.898 Regression 1 9.858769 9.858769 12.22345   r2 = 0.526341 Residual 11 8.872 0.806545       Total 12 18.73077           Using a = 0.05, Louis should ________________.

Which of the variables is the indepenent variable and dependent variable for the following question. fit a simple linear regression model to predict latitudes using average monthly range lat= latitudes range= the average monthly range between mean montly maximum and minimum temperatures for a selected set of US cities.