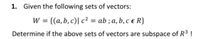
1. Given the following sets of vectors: W {(a,b, c)| c² = ab; a, b, c e R} %3D Determiine if the above sets of vectors are subs

1) Show that the following three vectors are coplanar. u=(2, 3,-1) v= (0, 1, -2) w=(2, 4, -3).

Let u, v, and w be vectors in R³. Given that v and w are linearly independent, but u, v and w are linearly dependent, what conclusions can we draw? Vectors v and w span a plane. u. (V x W) = 0. Vectors v + w and v- w are linearly independent. vxw = 0. Vector u is a linear combination of v and w.